12.8. Pie Menus
We are accustomed to using one-dimensional linear menus—not one-dimensional in appearance, but in usage. When a linear menu is posted, the cursor is positioned at the top of the menu and we are expected to move the cursor downward. If we overshoot the target menu item, we can move the cursor upward, but we're still moving in a single dimension. As the cursor moves over menu items, their reliefs change (unless disabled) to raised, meaning they are activated. To actually invoke a menu item we must release button 1 while the cursor is within the area defined by the menu item.
In contrast, pie menus are two dimensional: the cursor is initially positioned in the center of the pie, so all the wedge-shaped menu items are the same distance from the cursor but in different directions. Thus all menu items are equally accessible, spatially. Each pie piece has a virtual section that extends from the pie's perimeter to the edge of the display. To hit such a large target requires a gross, gestural motor movement, which your muscles easily learn and remember.
Pie menus were invented by Don Hopkins. For a history of Don's work, visit http://catalog.com/hopkins/piemenus/index.html. This experimental Perl/Tk pie menu implementation is based on a piece of Don's early work, written in 1992 for an early version of Tcl/Tk.
Figure 12-11 illustrates what a File pie menu might look like. The pie menu has six menu items, each occupying a 60 degree slice of the pie. To select an item, we just click anywhere on the pie piece (or the virtual part that extends to the display's edge). There's no need to be particularly accurate; just make a fast, casual motion. Notice that this pie menu has its menu items floating in space.

Figure 12-11. A pie menu with -shaped => 1
Figure 12-12 shows the same pie menu in a rectangular window with wedge dividers. Now, imagine those wedge dividers extending outwards to infinity (or as far as your arm is long or the display is big!). That huge pie slice defines the (virtual) pie menu item; you can click anywhere within that area!
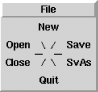
Figure 12-12. A pie menu with -shaped => 0
A pie menu is ideally suited for selecting two pieces of information simultaneously. Consider a word processor where we want to select a font and its size. Each font can be a pie piece, and its size is determined by how far from the center of the pie we click. Or think of a color wheel, where hue is a pie slice and its saturation varies from the pie's center to its circumference. Unfortunately, the current version of the Perl/Tk pie menu lacks this sophistication.
12.8.1. Fitts' Law
Pie menus are based on a model of human psychomotor behavior developed by P. M. Fitts. In his 1954 work, Fitts studied the time required to hit a target, based on target distance and size. Unsurprisingly, selecting a large menu item close at hand (a virtual pie menu item) with a mouse is faster than hunting for a small target far away (a tiny linear menu item).
We can write a Perl/Tk program to test this hypothesis. The basic idea is to start with the cursor at a known position, flash a target of random size and position, measure how long it takes to hit the target, and examine how this time depends on the target's distance and area. See Figure 12-13 for complete usage information.
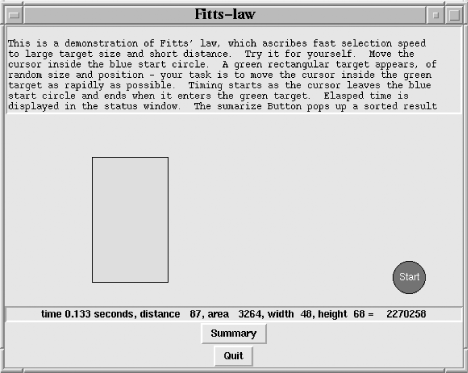
Figure 12-13. Demonstrating Fitts' law
The Fitts simulator uses a Canvas for the playing field, with a Canvas rectangle item as the target and an oval item as the starting point. The start circle is actually a canvas group[29] with a text item overlaid on top of the oval item. The group we'll tag with the string 'start' and the rectangle with the string 'rectangle', and we'll use those identifiers when addressing the canvas items.
[29] Tk 800.018 added the canvasGroup Canvas method. As the name might imply, many individual canvas items can be logically grouped together and referenced as a single entity, in a manner not unlike a mega-widget.
my $c = $mw->Canvas(qw/-width 500 -height 500/)->grid;
$c->createGroup(0, 0,
-tags => 'start',
-members => [
$c->createOval(qw/ 0 0 40 40 -fill blue/),
$c->createText(qw/20 20 -text Start -fill white/),
],
);These bindings give the simulation its proper behavior:
-
When the cursor enters the blue start circle, create the green target.
-
When the cursor leaves the blue start circle, record the current time.
-
When the cursor enters the green target, compute and display the elapsed time, and delete the target.
$c->bind('start', '<Enter>' => \&enter_start); $c->bind('start', '<Leave>' => \&leave_start); $c->bind('rectangle', '<Enter>' => \&enter_rectangle);
Prior to entering the main loop, seed the random number generator, used to generate random coordinates, and width and height values. The main loop essentially fetches two random numbers and treats them as an (x, y) pair specifying the start circle's top-left corner. The coords method changes the 'start' item's coordinates, effectively and instantaneously moving the item (group) to its new location. The waitVariable command (described in Chapter 15, "Anatomy of the MainLoop") then logically suspends the program, but still allows event processing, until the target receives an <Enter> event.
srand( time ^ $$ );
while (1) {
$rendezvous = 0;
my($x, $y) = points 2;
$c->coords('start', $x, $y);
$mw->waitVariable(\$rendezvous);
}Once the main loop has positioned the start circle, nothing happens until the cursor enters the circle. Once that happens, any rectangle is promptly deleted, which cures the pathological case of the user rapidly moving the cursor back and forth over the circle (hence generating multiple <Enter> events) and creating tons of rectangles. A random coordinate for the top-left corner of the rectangle is selected, as are random width/height values in the range 5 to 180, inclusive. Then the target is created and raised to ensure it's not obscured by the start circle.
sub enter_start {
my($c) = @_;
$c->delete('rectangle');
my $w = int(rand 180) + 5;
my $h = int(rand 180) + 5;
my($x, $y) = points 2;
$c->createRectangle($x, $y, $x+$w, $y+$h,
-fill => 'green', -tags => 'rectangle',
);
$c->raise(qw/rectangle start/);
$c->idletasks;
} # end enter_startNow the start circle and target rectangle are visible on the Canvas, yet nothing further happens until we move the cursor out of the circle (and generate a <Leave> event); only then does timing commence. The Tk::timeofday function returns the number of microseconds since the Tk program started.[30]
[30] That clock resolution may be a bit optimistic, but you can probably count on at least millisecond granularity.
sub leave_start {
$t0 = Tk::timeofday;
}At this point, we move the cursor to the target rectangle, which invokes the enter_rectangle callback. First, save the current time of day so we can compute the elapsed time. For the distance computation, we use the Pythagorean theorem that we all learned in high school. Since the start circle and target rectangle are both described by a bounding box, we can substitute the coordinates of the top-left corner in the distance equation. We mark this iteration of the simulation complete by modifying $rendezvous, which jogs the main loop into another iteration.
sub enter_rectangle {
my($c) = @_;
$t1 = Tk::timeofday( );
my(@rco) = $c->coords('rectangle');
my(@sco) = $c->coords('start');
my $dist = sqrt( ($sco[0] - $rco[0])**2 + ($sco[1] - $rco[1])**2 );
my $w = $rco[2] - $rco[0];
my $h = $rco[3] - $rco[1];
$stat = sprintf "time %5.3f seconds, distance % 4.d, " .
"area % 6.d, width %3.d, height %3.d = %10d",
$t1 - $t0, $dist, $w * $h, $w, $h
$rendezvous = 1;
} # end enter_rectangle
Copyright © 2002 O'Reilly & Associates. All rights reserved.