18.6 A Detour into Fractals
This chapter would be incomplete and dry without a small foray into Mandelbrot sets and the implementation of draw_mandel .
For starters, I highly recommend Ivars Peterson's book The Mathematical Tourist [ 13 ] for its engaging style and treatment of a surprisingly wide set of mathematical topics. We'll begin by assuming that you already know about complex numbers.
We know that a complex number a + b i is composed of two parts, the real part a , and the imaginary part b , that taken together constitute a point on a graph. Now consider the expression z = z 2 - 1 , where z is a complex number. We start with a complex number ( z 0 ) and plot it. We then substitute it in the above expression to produce a new complex number and plot this number. This exercise is repeated, say, 20 or 30 times. We find that different starting values of z 0 result either in this series trailing off to infinity, or remaining confined within a boundary. All z 0 's that result in a bounded series belong to a Julia set , named after the mathematician Gaston Julia. In other words, if we plot all the z 0 's that result in a bounded series, we will see a nice fractal picture (no, not the one we saw earlier).
Now, let us make the equation a bit more general:
z
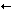 z
2
+
c
, where
c
is a complex number (the discussion above was for
c
= -1 + 0
i
). Now, if we plot the Julia sets for different values of
c
, we find that some plots show beautiful connected shapes while other disperse into a cloud of disconnected dots. Clearly, we are interested only in the former; all values of
c
that result in such nice-looking Julia sets are said to belong to the Mandelbrot set, after Benoit Mandelbrot.
z
2
+
c
, where
c
is a complex number (the discussion above was for
c
= -1 + 0
i
). Now, if we plot the Julia sets for different values of
c
, we find that some plots show beautiful connected shapes while other disperse into a cloud of disconnected dots. Clearly, we are interested only in the former; all values of
c
that result in such nice-looking Julia sets are said to belong to the Mandelbrot set, after Benoit Mandelbrot.
Calculating the Mandelbrot set is obviously a pain, because for every c (an infinite set), you have to plot the Julia set to see whether it disperses or not. Enter mathematicians John Hubbard and Adrien Douady. They proved that for a given value of c , it is enough to check whether a starting point of z 0 = 0 (that is, 0 + 0 i ) results in a bounded sequence. If it does, then that value of c yields a connected (nondispersing) Julia set. It has also been proven that all c 's belonging to the Mandelbrot set are contained within a small area that "looks like a small pimply snowman on his side," as Ivars Peterson puts it. This is the white central area inside Figure 18.3 , extending from -2 to +0.5 on the x -axis, and from -1.0 to +1.0 on the y -axis. So as soon as the series goes beyond 2, you know that it is not bounded, and, consequently, c is not going to be a part of the Mandelbrot set. To lend some more visual interest to the figure, we attempt to assign a color to every point within our viewing window, whether it belongs to the Mandelbrot set or not. Those that belong to this set are colored white, and those that don't are given a gray color, depending on how far the corresponding series attempts to jump out of the boundaries.
draw_mandel
(contained in the file
Fractal.c
and shown in
Example 18.3
) implements the algorithm described previously. The parameters are explained below, and the values that generated
Figure 18.3
are shown in parentheses:
- filename
-
The name of the GIF file to produce.
- width , height (400, 400)
-
The width and height of the GIF image in number of pixels.
- origin_real , origin_imag (-1.4,1.0)
-
What the top-left pixel corresponds to, given as a complex number.
- range (2.0)
-
The width and height spanned in the complex number plane. If the origin is -1.0 + 1.4 i and the range is 2, the figure spans -1.0 + 1.4 i to 1.0 - 0.6 i ( y decreases from top to bottom, x increases from left to right). If you reduce this number, the canvas is devoted to a smaller area of the complex plane. Consequently, range works as a zoom factor, the image varying inversely with this value.
- max_iterations (20)
-
The number of times one should iterate through z
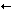 z
2
+ c before giving up to check before deciding whether the series is bounded.
z
2
+ c before giving up to check before deciding whether the series is bounded.
Example 18.3: mandel.c
#include <math.h>
#include <stdio.h>
#include <gd.h>
typedef struct {
double r, i;
} complex;
int draw_mandel (char *filename,
int width, int height,
double origin_real,
double origin_imag,
double range,
double max_iterations)
{
complex origin;
int colors[51], color, white, x, y, i;
FILE *out;
gdImagePtr im_out;
origin.r = origin_real; /* Measured from top-left */
origin.i = origin_imag;
if (!(out = fopen(filename, "wb"))) {
fprintf(stderr, "File %s could not be opened\n");
return 1;
}
im_out = gdImageCreate(width, height); /* Create a canvas */
/* Allocate some gray colors. Start from black, and increment r,g,b
values uniformly. This has the effect of varying the luminosity,
while keeping the same hue.
(Black = 0,0,0 and white = 255, 255,255 */
for (i = 0; i < 50; i++) {
color = i * 4;
colors[i] = gdImageColorAllocate(im_out, color,color,color);
}
white = gdImageColorAllocate(im_out, 255,255,255);
/* For each pixel on the canvas do ... */
for (y = 0; y < height; y++) {
for (x = 0; x < width; x++) {
complex z, c ;
int iter;
/* Convert the pixel to an equivalent complex number c,
given the origin and the range. The range acts like an
inverse zoom factor.*/
c.r = origin.r + (double) x / (double) width * range;
c.i = origin.i - (double) y / (double) height * range;
/* Examine each point calculated above to see if repeated
substitutions into an equation like z(next) = z**z + c
remains within a definite boundary.
If after <max_iterations> iterations it still hasn't gone
beyond the white area, it belongs to the Mandelbrot set.
But if it does, we assign it a color depending on how
far the series wants to jump out of bounds*/
color = white;
z.r = z.i = 0.0; /* Starting point */
for (iter = 0; iter < max_iterations; iter++) {
double dist, new_real, new_imag;
/*calculate z = z^2 + c */
/* Recall that z^2 is a^2 - b^2 + 2abi, if z = a + bi, */
new_real = z.r * z.r - z.i * z.i + c.r;
new_imag = 2 * z.r * z.i + c.i;
z.r = new_real; z.i = new_imag;
/* Pythagorean distance from 0,0 */
dist = new_real * new_real + new_imag * new_imag;
if (dist >= 4) {
/* No point on the mandelbrot set is more than 2 units
away from the origin. If it quits the boundary, give
that 'c' an interesting color depending on how far
the series wants to jump out of its bounds */
color = colors[(int) dist % i];
break;
}
}
gdImageSetPixel(im_out, x,y, color);
}
}
gdImageGif(im_out,out);
fclose(out);
return 0;
}