Chapter 16 TOC Chapter 18
Chapter 17. Data Structures
17.1 "Roses Are Red, Violets Are Blue; Lists Are Mutable, and So Is Class Foo"
Data structures are a central theme in most programs, whether you know it or not. It may not always be obvious, because Python provides a set of built-in types that make it easy to deal with structured data: lists, strings, tuples, dictionaries, and the like. For simple systems, these types are usually enough. Technically, dictionaries make many of the classical searching algorithms unnecessary in Python, and lists replace much of the work you'd do to support collections in lower-level languages. Both are so easy to use, though, that you generally never give them a second thought.
But for advanced applications, we may need to add more sophisticated types of our own to handle extra requirements. In this chapter, we'll explore a handful of advanced data structure implementations in Python: sets, stacks, graphs, and so on. As we'll see, data structures take the form of new object types in Python, integrated into the language's type model. That is, objects we code in Python become full-fledged datatypes -- they can look and feel just like built-in lists, numbers, and dictionaries, to the scripts that use them.
Although the examples in this chapter illustrate advanced programming techniques, they also underscore Python's support for writing reusable software. By coding object implementations with classes, modules, and other Python tools, they naturally become generally useful components, which may be used in any program that imports them. In effect, we will be building libraries of data structure classes, whether we plan for it or not.
In addition, although the examples in this chapter are pure Python code, we will also be building a path towards the next part of the book here. From the most general perspective, new Python objects can be implemented in either Python or an integrated language such as C. In particular, pay attention to the stack objects implemented in the first section of this chapter; they will later be reimplemented in C to gauge both the benefits and complexity of C migration.
17.2 Implementing Stacks
Stacks are a common and straightforward data structure, used in a variety of applications: language processing, graph searches, etc. In short, stacks are a last-in-first-out collection of objects: the last item added to the collection is always the next one to be removed. Clients use stacks by:
· Pushing items onto the top
· Popping items off the top
Depending on client requirements, there may also be tools for such tasks as testing if the stack is empty, fetching the top item without popping it, iterating over a stack's items, testing for item membership, etc.
In Python, a simple list is often adequate for implementing a stack: because we can change lists in place, we can either add and delete items from the front (left) or end (right). Table 17-1 summarizes various built-in operations available for implementing stack-like behavior with Python lists, depending on whether the stack "top" is the first or last node in the list. In this table, string 'c' is the top item on the stack.
Table 17-1. Stacks as Lists |
|||
|
Operation |
Top
is end-of-list |
Top
is front-of-list |
Top
is front-of-list |
|
New |
stack=['a','b','c'] |
stack=['c','b','a'] |
stack=['c','b','a'] |
|
Push |
stack.append('d') |
stack.insert(0,'d') |
stack[0:0] =
['d'] |
|
Pop[1] |
X =
stack[-1]; del stack[-1] |
x = stack[0]; del stack[:1] |
x = stack[0]; stack[:1] =
[] |
This list arrangement works and will be relatively fast. But it also binds stack-based programs to the stack representation chosen: stack operations will all be hardcoded. If we later want to change how a stack is represented, or extend its basic operations, we're stuck: every stack-based program will have to be updated.
For instance, to add logic that monitors the number of stack operations a program performs, we'd have to add code around each hardcoded stack operation. In a large system, this operation may be nontrivial. As we'll see in the next chapter, we may also decide to move stacks to a C-based implementation, if they prove to be a performance bottleneck. As a general rule, hardcoded operations on built-in data structures don't support future migrations as well as we'd sometimes like.
17.2.1 A Stack Module
Perhaps a better approach is to encapsulate stack implementations using Python's code reuse tools. Let's begin by implementing a stack as a module containing a Python list, plus functions to operate on it (see Example 17-1).
Example 17-1. PP2E\Dstruct\Basic\stack1.py
stack = [] # on first importerror = 'stack1.error' # local exceptionsdef push(obj):
global stack # use 'global' to change
stack = [obj] + stack # add item to the front
def pop( ):
global stack if not stack:raise error, 'stack underflow' # raise local error
top, stack = stack[0], stack[1:] # remove item at front
return topdef top( ):if not stack: # raise local error
raise error, 'stack underflow' # or let IndexError occur
return stack[0] def empty( ): return not stack # is the stack []?
def member(obj): return obj in stack # item in stack?
def item(offset): return stack[offset] # index the stackdef length( ): return len(stack) # number entries
def dump( ): print '<Stack:%s>' % stack
This module creates a list object (stack) and exports functions to manage access to it. The stack is declared global in functions that change it, but not in those that just reference it. The module also defines an error object (error) that can be used to catch exceptions raised locally in this module. Some stack errors are built-in exceptions: method item triggers IndexError for out-of-bounds indexes.
Most of the stack's functions just delegate the operation to the embedded list used to represent the stack. In fact, the module is really just a wrapper around a Python list. But this extra layer of interface logic makes clients independent of the actual implementation of the stack. So, we're able to change the stack later without impacting its clients.
As usual, one of the best ways to understand such code is to see it in action. Here's an interactive session that illustrates the module's interfaces:
C:\...\PP2E\Dstruct\Basic>python
>>> import stack1
>>> stack1.push('spam')>>> stack1.push(123)
>>> stack1.top( )123
>>> stack1.stack
[123, 'spam']
>>> stack1.pop( )123
>>> stack1.dump( )<Stack:['spam']>
>>> stack1.pop( )'spam'
>>> stack1.empty( )1
>>> for c in 'spam': stack1.push(c)
...
>>> while not stack1.empty( ):... print stack1.pop( ),
...
m a p s
Other operations are analogous, but the main thing to notice here is that all stack operations are module functions. For instance, it's possible to iterate over the stack, but we need to use counter-loops and indexing function calls (item ). There's nothing preventing clients from accessing (and changing) stack1.stack directly, but doing so defeats the purpose of interfaces like this one.
17.2.2 A Stack Class
Perhaps the biggest drawback of the module-based stack is that it supports only a single stack object. All clients of the stack module effectively share the same stack. Sometimes we want this feature: a stack can serve as a shared-memory object for multiple modules. But to implement a true stack datatype, we need to use classes.
To illustrate, let's define a full-featured stack class. The Stack class shown in Example 17-2 defines a new datatype, with a variety of behavior. Like the module, the class uses a Python list to hold stacked objects. But this time, each instance gets its own list. The class defines both "real" methods, and specially named methods that implement common type operations. Comments in the code describe special methods.
Example 17-2. PP2E\Dstruct\Basic\stack2.py
error = 'stack2.error' # when imported: local exceptionclass Stack:
def __init__(self, start=[]): # self is the instance object
self.stack = [] # start is any sequence: stack..
for x in start: self.push(x) self.reverse( ) # undo push's order reversal
def push(self, obj): # methods: like module + self
self.stack = [obj] + self.stack # top is front of list
def pop(self):
if not self.stack: raise error, 'underflow'
top, self.stack = self.stack[0], self.stack[1:] return top def top(self): if not self.stack: raise error, 'underflow' return self.stack[0] def empty(self):return not self.stack # instance.empty( )
# overloads def __repr__(self):return '[Stack:%s]' % self.stack # print, backquotes,..
def __cmp__(self, other):
return cmp(self.stack, other.stack) # '==', '>, '<=', '!=',..
def __len__(self): return len(self.stack) # len(instance), not instance
def __add__(self, other): return Stack(self.stack + other.stack) # instance1 + instance2
def __mul__(self, reps): return Stack(self.stack * reps) # instance * reps
def __getitem__(self, offset):
return self.stack[offset] # intance[offset], in, for
def __getslice__(self, low, high):
return Stack(self.stack[low : high]) # instance[low:high]
def __getattr__(self, name):return getattr(self.stack, name) # instance.sort()/reverse( )/..
Now distinct instances are created by calling the Stack class like a function. In most respects, the Stack class implements operations exactly like the stack module in Example 17-1. But here, access to the stack is qualified by self, the subject instance object. Each instance has its own stack attribute, which refers to the instance's own list. Furthermore, instance stacks are created and initialized in the __init__ constructor method, not when the module is imported. Let's make a couple of stacks to see how this all works in practice:
>>> from stack2 import Stack
>>> x = Stack( ) # make a stack object, push items
>>> x.push('spam')>>> x.push(123)
>>> x # __repr__ prints a stack[Stack:[123, 'spam']]
>>> y = Stack( ) # two distinct stacks objects
>>> y.push(3.1415) # they do not share content>>> y.push(x.pop( ))>>> x, y
([Stack:['spam']], [Stack:[123, 3.1415]])
>>> z = Stack( ) # third distinct stack object
>>> for c in 'spam': z.push(c)
...
>>> while z: print z.pop( ), # __len__ tests stack truth
...
m a p s
>>> z = x + y # __add__ handles stack +>>> z # holds three different types[Stack:['spam', 123, 3.1415]]
>>> for item in z: print item, # __getitem__ does for...
spam 123 3.1415
Like lists and dictionaries, Stack defines both methods and operators for manipulating instances by attribute qualification and expressions. Additionally, it defines the __getattr__ metaclass method to intercept references to attributes not defined in the class and to route them to the wrapped list object (to support list methods: sort, append, reverse, etc.). Many of the module's operations become operators in the class. Table 17-2 shows the equivalence of module and class operations (columns 1 and 2) and gives the class method that comes into play for each (column 3).
Table 17-2. Module/Class Operation Comparison |
||
|
Module
Operations |
Class
Operations |
Class
Method |
|
module.empty(
) |
not instance |
__len__ |
|
module.member(x) |
x in instance |
__getitem__ |
|
module.item(i) |
instance[i] |
__getitem__ |
|
module.length(
) |
len(instance) |
__len__ |
|
module.dump(
) |
print
instance |
__repr__ |
|
range( ) counter loops |
for x in
instance |
__getitem__ |
|
manual
loop logic |
instance +
instance |
__add__ |
|
module.stack.reverse(
) |
instance.reverse(
) |
__getattr__ |
|
module.push/pop/top |
instance.push/pop/top |
push/pop/top |
In effect, classes let us extend Python's set of built-in types with reusable types implemented in Python modules. Class-based types may be used just like built-in types: depending on which operation methods they define, classes can implement numbers, mappings, and sequences, and may be mutable or not. Class-based types may also fall somewhere in between these categories.
17.2.3 Customization: Performance Monitors
So far we've seen how classes support multiple instances and integrate better with Python's object model by defining operator methods. One of the other main reasons for using classes is to allow for future extensions and customizations. By implementing stacks with a class, we can later add subclasses that specialize the implementation for new demands.
For instance, suppose we've started using the Stack class in Example 17-2, but we start running into performance problems. One way to isolate bottlenecks is to instrument data structures with logic that keeps track of usage statistics, which we can analyze after running client applications. Because Stack is a class, we can add such logic in a new subclass, without affecting the original stack module (or its clients). The subclass in Example 17-3 extends Stack to keep track of overall push/pop usage frequencies and to record the maximum size of each instance.
Example 17-3. PP2E\Dstruct\Basic\stacklog.py
from stack2 import Stack # extends imported Stack
class StackLog(Stack): # count pushes/pops, max-sizepushes = pops = 0 # shared/static class members
def __init__(self, start=[]): # could also be module vars
self.maxlen = 0 Stack.__init__(self, start) def push(self, object): Stack.push(self, object) # do real push
StackLog.pushes = StackLog.pushes + 1 # overall stats
self.maxlen = max(self.maxlen, len(self)) # per-instance stats
def pop(self):
StackLog.pops = StackLog.pops + 1 # overall counts
return Stack.pop(self) # not 'self.pops': instance
def stats(self):return self.maxlen, self.pushes, self.pops # get counts from instance
This subclass works the same as the original Stack; it just adds monitoring logic. The new stats method is used to get a statistics tuple through an instance:
>>> from stacklog import StackLog
>>> x = StackLog( )>>> y = StackLog( ) # make two stack objects
>>> for i in range(3): x.push(i) # and push object on them...
>>> for c in 'spam': y.push(c)...
>>> x, y # run inherited __repr__
([Stack:[2, 1, 0]], [Stack:['m', 'a', 'p', 's']])
>>> x.stats(), y.stats( )((3, 7, 0), (4, 7, 0))
>>>
>>> y.pop(), x.pop( )('m', 2)>>> x.stats(), y.stats( ) # my maxlen, all pushes, all pops
((3, 7, 2), (4, 7, 2))
Notice the use of class attributes to record overall pushes and pops, and instance attributes for per-instance maximum length. By hanging attributes on different objects, we can expand or narrow their scopes.
17.2.4 Optimization: Tuple Tree Stacks
One of the nice things about wrapping objects up in classes is that you are free to change the underlying implementation without breaking the rest of your program. Optimizations can be added in the future, for instance, with minimal impact; the interface is unchanged, even if the internals are. There are a variety of ways to implement stacks, some more efficient than others. So far, our stacks have used slicing and concatenation to implement pushing and popping. This method is relatively inefficient: both operations make copies of the wrapped list object. For large stacks, this practice can add a significant time penalty.
One way to speed up such code is to change the underlying data structure completely. For example, we can store the stacked objects in a binary tree of tuples: each item may be recorded as a pair: (object, tree), where object is the stacked item, and tree is either another tuple pair giving the rest of the stack or None to designate an empty stack. A stack of items [1,2,3,4] would be internally stored as a tuple tree (1,(2,(3,(4,None)))).
This tuple-based representation is similar to the notion of "cons-cells" in Lisp-family languages: the object on the left is the car, and the rest of the tree on the right is the cdr. Because we add or remove only a top tuple to push and pop items, this structure avoids copying the entire stack. For large stacks, the benefit might be significant. The next class, shown in Example 17-4, implements these ideas.
Example 17-4. PP2E\Dstruct\Basic\stack3.py
class Stack:
def __init__(self, start=[]): # init from any sequence
self.stack = None # even other (fast)stacks
for i in range(-len(start), 0): self.push(start[-i - 1]) # push in reverse order
def push(self, node): # grow tree 'up/left'
self.stack = node, self.stack # new root tuple: (node, tree)
def pop(self): node, self.stack = self.stack # remove root tuple
return node # TypeError if empty
def empty(self): return not self.stack # is it 'None'?
def __len__(self): # on: len, not
len, tree = 0, self.stack while tree:len, tree = len+1, tree[1] # visit right subtrees
return lendef __getitem__(self, index): # on: x[i], in, for
len, tree = 0, self.stackwhile len < index and tree: # visit/count nodes
len, tree = len+1, tree[1] if tree:return tree[0] # IndexError if out-of-bounds
else: raise IndexError # so 'in' and 'for' stop
def __repr__(self): return '[FastStack:' + `self.stack` + ']'
This class's __getitem__ method handles indexing, in tests, and for loop iteration as before, but this version has to traverse a tree to find a node by index. Notice that this isn't a subclass of the original Stack class. Since nearly every operation is implemented differently here, inheritance won't really help. But clients that restrict themselves to the operations that are common to both classes can still use them interchangeably -- they just need to import a stack class from a different module to switch implementations. Here's a session with this stack version; as long as we stick to pushing, popping, indexing, and iterating, this version is essentially indistinguishable from the original:
>>> from stack3 import Stack
>>> x = Stack( )>>> y = Stack( )>>> for c in 'spam': x.push(c)
...
>>> for i in range(3): y.push(i)
...
>>> x
[FastStack:('m', ('a', ('p', ('s', None))))]>>> y
[FastStack:(2, (1, (0, None)))]
>>> len(x), x[2], x[-1]
(4, 'p', 'm')
>>> x.pop( )'m'
>>> x
[FastStack:('a', ('p', ('s', None)))]>>>
>>> while y: print y.pop( ),...
2 1 0
17.2.5 Optimization: In-place List Modifications
Perhaps a better way to speed up the stack object, though, is to fall back on the mutability of Python's list object. Because lists can be changed in place, they can be modified more quickly than any of the prior examples. In-place change operations like append are prone to complications when a list is referenced from more than one place. But because the list inside the stack object isn't meant to be used directly, we're probably safe here. The module in Example 17-5 shows one way to implement a stack with in-place changes; some operator overloading methods have been dropped to keep this simple. The new Python pop method it uses is equivalent to indexing and deleting the item at offset -1 (top is end-of-list here).
Example 17-5. PP2E\Dstruct\Basic\stack4.py
error = 'stack4.error' # when imported: local exceptionclass Stack:
def __init__(self, start=[]): # self is the instance object
self.stack = [] # start is any sequence: stack..
for x in start: self.push(x) def push(self, obj): # methods: like module + self
self.stack.append(obj) # top is end of list
def pop(self):
if not self.stack: raise error, 'underflow'return self.stack.pop( ) # like fetch and delete stack[-1]
def top(self): if not self.stack: raise error, 'underflow' return self.stack[-1]def empty(self):
return not self.stack # instance.empty( )
def __len__(self): return len(self.stack) # len(instance), not intance
def __getitem__(self, offset):
return self.stack[offset] # instance[offset], in, for
def __repr__(self): return '[Stack:%s]' % self.stack
This version works like the original in module stack2, too -- just replace stack2 with stack4 in the previous interaction to get a feel for its operation. The only obvious difference is that stack items are in reverse when printed (i.e., the top is the end):
>>> from stack4 import Stack
>>> x = Stack( )>>> x.push('spam')>>> x.push(123)
>>> x
[Stack:['spam', 123]]
>>>
>>> y = Stack( )>>> y.push(3.1415)
>>> y.push(x.pop( ))>>> x, y
([Stack:['spam']], [Stack:[3.1415, 123]])
>>> y.top( )123
17.2.6 Timing the Improvements
The in-place changes stack object probably runs faster than both the original and the tuple-tree version, but the only way to really be sure how much faster is to time the alternative implementations. Since this could be something we'll want to do more than once, let's first define a general module for timing functions in Python. In Example 17-6, the built-in time module provides a clock function that we can use to get the current CPU time in floating-point seconds, and the function timer.test simply calls a function reps times and returns the number of elapsed seconds by subtracting stop from start CPU times.
Example 17-6. PP2E\Dstruct\Basic\timer.py
def test(reps, func, *args):
import timestart = time.clock( ) # current CPU tim in float seconds
for i in xrange(reps): # call function reps times
apply(func, args) # discard any return value
return time.clock( ) - start # stop time - start time
Next, we define a test driver script (see Example 17-7). It expects three command-line arguments: the number of pushes, pops, and indexing operations to perform (we'll vary these arguments to test different scenarios). When run at the top level, the script creates 200 instances of the original and optimized stack classes, and performs the specified number of operations on each stack.[2] Pushes and pops change the stack; indexing just accesses it.
Example 17-7. PP2E\Dstruct\Basic\stacktime.py
import stack2 # list-based stacks: [x]+yimport stack3 # tuple-tree stacks: (x,y)import stack4 # in-place stacks: y.append(x)
import timer # general function timer functionrept = 200
from sys import argv
pushes, pops, items = eval(argv[1]), eval(argv[2]), eval(argv[3])
def stackops(stackClass):
#print stackClass.__module__x = stackClass('spam') # make a stack object
for i in range(pushes): x.push(i) # exercise its methods
for i in range(items): t = x[i]
for i in range(pops): x.pop( )
print 'stack2:', timer.test(rept, stackops, stack2.Stack) # pass class to testprint 'stack3:', timer.test(rept, stackops, stack3.Stack) # rept*(push+pop+ix)print 'stack4:', timer.test(rept, stackops, stack4.Stack)
Here are some of the timings reported by the test driver script. The three outputs represent the measured run times in seconds for the original, tuple, and in-place stacks. For each stack type, the first test creates 200 stack objects and performs roughly 120,000 stack operations (200 rept x (200 pushes + 200 indexes + 200 pops)), in the test duration times listed. These results were obtained on a 650 MHz Pentium III Windows machine, and a Python 1.5.2 install:
C:\...\PP2E\Dstruct\Basic>python stacktime.py 200 200 200
stack2: 1.67890008213
stack3: 7.70020952413
stack4: 0.694291724635
C:\...\PP2E\Dstruct\Basic>python stacktime.py 200 50 200
stack2: 1.06876246669
stack3: 7.48964866994
stack4: 0.477584270605
C:\...\PP2E\Dstruct\Basic>python stacktime.py 200 200 50
stack2: 1.34536448817
stack3: 0.795615917129
stack4: 0.57297976835
C:\...\PP2E\Dstruct\Basic>python stacktime.py 200 200 0
stack2: 1.33500477715
stack3: 0.300776077373
stack4: 0.533050336077
If you look closely enough, you'll notice that the results show that the tuple-based stack (stack3) performs better when we do more pushing and popping, but worse if we do much indexing. Indexing lists is extremely fast for built-in lists, but very slow for tuple trees -- the Python class must traverse the tree manually. The in-place change stacks (stack4) are almost always fastest, unless no indexing is done at all -- tuples won by a hair in the last test case. Since pushes and pops are most of what clients would do to a stack, tuples are a contender, despite their poor indexing performance. Of course, we're talking about fractions of a second after many tens of thousands of operations; in many applications, your users probably won't care either way.
17.3 Implementing Sets
Another commonly used data structure is the set, a collection of objects that support operations such as:
Intersection
Make a new set with all items in common.
Union
Make a new set with all items in either operand.
Membership
Test if an item exists in a set.
And there are others, depending on the intended use. Sets come in handy for dealing with more abstract group combinations. For instance, given a set of engineers and a set of writers, you can pick out individuals who do both activities by intersecting the two sets. A union of such sets would contain either type of individual, but only include any given individual once.
Python lists, tuples, and strings come close to the notion of a set: the in operator tests membership, for iterates, etc. Here, we add operations not directly supported by Python sequences. The idea is that we're extending built-in types for unique requirements.
17.3.1 Set Functions
As before, let's first start out with a function-based set manager. But this time, instead of managing a shared set object in a module, let's define functions to implement set operations on passed-in Python sequences (see Example 17-8).
Example 17-8. PP2E\Dstruct\Basic\inter.py
def intersect(seq1, seq2):
res = [] # start with an empty list
for x in seq1: # scan the first sequence
if x in seq2:res.append(x) # add common items to the end
return resdef union(seq1, seq2): res = list(seq1) # make a copy of seq1
for x in seq2: # add new items in seq2
if not x in res: res.append(x) return res
These functions work on any type of sequence -- lists strings, tuples, and other objects that conform to the sequence protocols expected by these functions (for loops, in membership tests). In fact, we can even use them on mixed object types: the last two commands in the following code compute the intersection and union of a list and a tuple. As usual in Python, the object interface is what matters, not the specific types:
C:\...\PP2E\Dstruct\Basic>python
>>> from inter import *
>>> s1 = "SPAM"
>>> s2 = "SCAM"
>>> intersect(s1, s2), union(s1, s2)
(['S', 'A', 'M'], ['S', 'P', 'A', 'M', 'C'])
>>> intersect([1,2,3], (1,4))
[1]
>>> union([1,2,3], (1,4))
[1, 2, 3, 4]
Notice that the result is always a list here, regardless of the type of sequences passed in. We could work around this by converting types or by using a class to sidestep this issue (and we will in a moment). But type conversions aren't clear- cut if the operands are mixed-type sequences. Which type do we convert to?
17.3.1.1 Supporting multiple operands
If we're going to use the intersect and union functions as general tools, one useful extension is support for multiple arguments (i.e., more than two). The functions in Example 17-9 use Python's variable-length argument lists feature to compute the intersection and union of arbitrarily many operands.
Example 17-9. PP2E\Dstruct\Basic\inter2.py
def intersect(*args):
res = [] for x in args[0]: # scan the first list
for other in args[1:]: # for all other arguments
if x not in other: break # this item in each one?
else:res.append(x) # add common items to the end
return resdef union(*args): res = []for seq in args: # for all sequence-arguments
for x in seq: # for all nodes in argument
if not x in res: res.append(x) # add new items to result
return res
The multi-operand functions work on sequences in the same way as the original functions, but they support three or more operands. Notice that the last two examples in the following session work on lists with embedded compound objects: the in tests used by the intersect and union functions apply equality testing to sequence nodes recursively, as deep as necessary to determine collection comparison results:
C:\...\PP2E\Dstruct\Basic>python
>>> from inter2 import *
>>> s1, s2, s3 = 'SPAM', 'SLAM', 'SCAM'
>>> intersect(s1, s2)
['S', 'A', 'M']
>>> intersect(s1, s2, s3)
['S', 'A', 'M']
>>> intersect(s1, s2, s3, 'HAM')
['A', 'M']
>>> union(s1, s2), union(s1, s2, s3)
(['S', 'P', 'A', 'M', 'L'], ['S', 'P', 'A', 'M', 'L', 'C'])
>>> intersect([1,2,3], (1,4), range(5))
[1]
>>> s1 = (9, (3.14, 1), "bye", [1,2], "mello")
>>> s2 = [[1,2], "hello", (3.14, 0), 9]
>>> intersect(s1, s2)
[9, [1, 2]]
>>> union(s1, s2)
[9, (3.14, 1), 'bye', [1, 2], 'mello', 'hello', (3.14, 0)]
17.3.2 Set Classes
The set functions can operate on a variety of sequences, but they aren't as friendly as true objects. Among other things, your scripts need to keep track of the sequences passed into these functions manually. Classes can do better: the class in Example 17-10 implements a set object that can hold any type of object. Like the stack classes, it's essentially a wrapper around a Python list with extra set operations.
Example 17-10. PP2E\Dstruct\Basic\set.py
class Set:
def __init__(self, value = []): # on object creation
self.data = [] # manages a local list
self.concat(value)def intersect(self, other): # other is any sequence type
res = [] # self is the instance subject
for x in self.data: if x in other: res.append(x)return Set(res) # return a new Set
def union(self, other):
res = self.data[:] # make a copy of my list
for x in other:
if not x in res: res.append(x)return Set(res)
def concat(self, value): # value: a list, string, Set...
for x in value: # filters out duplicates
if not x in self.data: self.data.append(x)def __len__(self): return len(self.data)
def __getitem__(self, key): return self.data[key]
def __and__(self, other): return self.intersect(other)
def __or__(self, other): return self.union(other)
def __repr__(self): return '<Set:' + `self.data` + '>'
The Set class is used like the Stack class we saw earlier in this chapter: we make instances and apply sequence operators plus unique set operations to them. Intersection and union can be called as methods, or by using the & and | operators normally used for built-in integer objects. Because we can string operators in expressions now (e.g., x & y & z), there is no obvious need to support multiple operands in intersect/union methods here. As with all objects, we can either use the Set class within a program, or test it interactively as follows:
>>> from set import Set
>>> users1 = Set(['Bob', 'Emily', 'Howard', 'Peeper'])
>>> users2 = Set(['Jerry', 'Howard', 'Carol'])
>>> users3 = Set(['Emily', 'Carol'])
>>> users1 & users2
<Set:['Howard']>
>>> users1 | users2
<Set:['Bob', 'Emily', 'Howard', 'Peeper', 'Jerry', 'Carol']>
>>> users1 | users2 & users3
<Set:['Bob', 'Emily', 'Howard', 'Peeper', 'Carol']>
>>> (users1 | users2) & users3
<Set:['Emily', 'Carol']>
>>> users1.data
['Bob', 'Emily', 'Howard', 'Peeper']
17.3.3 Optimization: Moving Sets to Dictionaries
Once you start using the Set class, the first problem you might encounter is its performance: its nested for loops and in scans become exponentially slow. That slowness may or may not be significant in your applications, but library classes should generally be coded as efficiently as possible.
One way to optimize set performance is by changing the implementation to use dictionaries instead of lists, for storing sets internally -- items may be stored as the keys of a dictionary whose values are all None. Because lookup time is constant and short for dictionaries, the in list scans of the original set may be replaced with direct dictionary fetches in this scheme. In traditional terms, moving sets to dictionaries replaces slow linear searches with fast hash tables.
The module in Example 17-11 implements this idea. Its class is a subclass of the original set, and redefines the methods that deal with the internal representation but inherits others. The inherited & and | methods trigger the new intersect and union methods here, and the inherited len method works on dictionaries as is. As long as Set clients are not dependent on the order of items in a set, they can switch to this version directly by just changing the name of the module where Set is imported from; the class name is the same.
Example 17-11. PP2E\Dstruct\Basic\fastset.py
import set
# fastset.Set extends set.Set
class Set(set.Set):
def __init__(self, value = []):self.data = {} # manages a local dictionary
self.concat(value) # hashing: linear search times
def intersect(self, other): res = {}for x in other: # other: a sequence or Set
if self.data.has_key(x): # use hash-table lookup
res[x] = Nonereturn Set(res.keys( )) # a new dictionary-based Set
def union(self, other):
res = {} # other: a sequence or Set
for x in other: # scan each set just once
res[x] = Nonefor x in self.data.keys( ): # '&' and '|' come back here
res[x] = None # so they make new fastset's
return Set(res.keys( ))
def concat(self, value): for x in value: self.data[x] = None # inherit and, or, lendef __getitem__(self, key): return self.data.keys( )[key]
def __repr__(self): return '<Set:' + `self.data.keys( )` + '>'
This works about the same as the previous version:
>>> from fastset import Set
>>> users1 = Set(['Bob', 'Emily', 'Howard', 'Peeper'])
>>> users2 = Set(['Jerry', 'Howard', 'Carol'])
>>> users3 = Set(['Emily', 'Carol'])
>>> users1 & users2
<Set:['Howard']>
>>> users1 | users2
<Set:['Emily', 'Howard', 'Jerry', 'Carol', 'Peeper', 'Bob']>
>>> users1 | users2 & users3
<Set:['Emily', 'Howard', 'Carol', 'Peeper', 'Bob']>
>>> (users1 | users2) & users3
<Set:['Emily', 'Carol']>
>>> users1.data
{'Emily': None, 'Bob': None, 'Peeper': None, 'Howard': None}
The main functional difference in this version is the order of items in the set: because dictionaries are randomly ordered, this set's order will differ from the original. For instance, you can store compound objects in sets, but the order of items varies in this version:
>>> import set, fastset
>>> a = set.Set([(1,2), (3,4), (5,6)])
>>> b = set.Set([(3,4), (7,8)])
>>> a & b
<Set:[(3, 4)]>
>>> a | b
<Set:[(1, 2), (3, 4), (5, 6), (7, 8)]>
>>> a = fastset.Set([(1,2), (3,4), (5,6)])
>>> b = fastset.Set([(3,4), (7,8)])
>>> a & b
<Set:[(3, 4)]>
>>> a | b
<Set:[(3, 4), (1, 2), (7, 8), (5, 6)]>
>>> b | a
<Set:[(3, 4), (5, 6), (1, 2), (7, 8)]>
Sets aren't supposed to be ordered anyhow, so this isn't a showstopper. A deviation that might matter, though, is that this version cannot be used to store unhashable objects. This stems from the fact that dictionary keys must be immutable. Because values are stored in keys, dictionary sets can contain only things like tuples, strings, numbers, and class objects with immutable signatures. Mutable objects like lists and dictionaries won't work directly. For example, the call:
fastset.Set([[1,2],[3,4]])
raises an exception with this dictionary-based set, but works with the original set class. Tuples work here because they are immutable; Python computes hash values and tests key equality as expected.
17.3.3.1 Timing the results
So how did we do on the optimization front? Example 17-12 contains a script to compare set class performance. It reuses the timer module used earlier to test stacks.
Example 17-12. PP2E\Dstruct\Basic\settime.py
import timer, sys
import set, fastset
def setops(Class):
a = Class(range(50)) # a 50-integer set
b = Class(range(20)) # a 20-integer set
c = Class(range(10))
d = Class(range(5)) for i in range(5):t = a & b & c & d # 3 intersections
t = a | b | c | d # 3 unions
if __name__ == '__main__':
rept = int(sys.argv[1]) print 'set => ', timer.test(rept, setops, set.Set)
print 'fastset =>', timer.test(rept, setops, fastset.Set)
The setops function makes four sets and combines them with intersection and union operators five times. A command-line argument controls the number of times this whole process is repeated. More accurately, each call to setops makes 34 Set instances (4 + [5 x (3 + 3)] ), and runs the intersect and union methods 15 times each (5 x 3) in the for loop's body. On the same test machine, the performance improvement is equally dramatic this time around:
C:\...\PP2E\Dstruct\Basic>python settime.py 50
set => 1.5440352671fastset => 0.446057593993
C:\...\PP2E\Dstruct\Basic>python settime.py 100
set => 2.77783486146fastset => 0.888354648921
C:\...\PP2E\Dstruct\Basic>python settime.py 200
set => 5.7762634305fastset => 1.77677885985
At least for this test case, the simple set implementation is over three times slower than dictionary-based sets. In fact, this threefold speedup is probably sufficient. Python dictionaries are already optimized hash tables that you might be hard- pressed to improve on. Unless there is evidence that dictionary-based sets are still too slow, our work here is probably done.
Using the Python ProfilerThe Python profiler provides another way to gather performance data besides timing sections of code as done in this chapter. Because the profiler tracks all function calls, it provides much more information in a single blow. As such, it's a more powerful way to isolate bottlenecks in slow programs -- after profiling, you should have a good idea where to focus your optimization efforts. The profiler ships with Python as the standard library module called profile, and provides a variety of interfaces for measuring code performance. It is structured and used much like the pdb command-line debugger: import the profile module and call its functions with a code string to measure performance. The simplest profiling interface is its profile.run(statementstring) function. When invoked, the profiler runs the code string, collects statistics during the run, and issues a report on the screen when the statement completes. The report's format is straightforward and well-documented in the Python library manual. By default, it lists the number of calls and times spent in each function invoked during the run. When the profiler is enabled, each interpreter event is routed to a Python handler. This gives an accurate picture of performance, but tends to make the program being profiled run much slower than normal. |
17.3.4 Optimizing fastset by Coding Techniques (or Not)
As coded, there seems to be a bottleneck in the fastset class: each time we call a dictionary's keys method, Python makes a new list to hold the result, and this can happen repeatedly during intersections and unions. If you are interested in trying to optimize this further, see the following files in the book CD (view CD-ROM content online at http://examples.oreilly.com/python2):
· PP2E\Dstruct\Basic\fastset2.py
· PP2E\Dstruct\Basic\fastset3.py
I wrote these to try to speed up sets further, but failed miserably. It turns out that adding extra code to try to shave operations usually negates the speedup you obtain. There may be faster codings, but the biggest win here was likely in changing the underlying data structure to dictionaries, not in minor code tweaks.
As a rule of thumb, your intuition about performance is almost always wrong in a dynamic language like Python: the algorithm is usually the real culprit behind performance problems, not the coding style or even the implementation language. By removing the combinatorial list scanning algorithm of the original set class, the Python implementation became dramatically faster.
In fact, moving the original set class to C without fixing the algorithm would not have addressed the real performance problem. Coding tricks don't usually help as much either, and they make your programs difficult to understand. In Python, it's almost always best to code for readability first and optimize later if needed. Despite its simplicity, fastset is fast indeed.
17.3.5 Adding Relational Algebra to Sets (CD)
If you are interested in studying additional set-like operations coded in Python, see the following files on this book's CD (see http://examples.oreilly.com/python2):
· PP2E\Dstruct\Basic\rset.py : RSet implementation
· PP2E\Dstruct\Basic\reltest.py : Test script for RSet
The RSet subclass defined in rset.py adds basic relational algebra operations for sets of dictionaries. It assumes the items in sets are mappings (rows), with one entry per column (field). RSet inherits all the original Set operations (iteration, intersection, union, & and | operators, uniqueness filtering, etc.), and adds new operations as methods:
Select
Return a set of nodes that have a field equal to a given value.
Bagof
Collect set nodes that satisfy an expression string.
Find
Select tuples according to a comparison, field, and value.
Match
Find nodes in two sets with the same values for common fields.
Product
Compute a Cartesian product: concatenate tuples from two sets.
Join
Combine tuples from two sets that have the same value for a field.
Project
Extract named fields from the tuples in a table.
Difference
Remove one set's tuples from another.
Alternative implementations of set difference operations can also be found in the diff.py file in the same CD directory.
17.4 Binary Search Trees
Binary trees are a data structure that impose an order on inserted nodes: items less than a node are stored in its left subtree, and items greater than a node are inserted in the right. At the bottom, the subtrees are empty. Because of this structure, binary trees naturally support quick, recursive traversals -- at least ideally, every time you follow a link to a subtree, you divide the search space in half.[3]
Binary trees are named for the implied branch-like structure of their subtree links. Typically, their nodes are implemented as a triple of values: (LeftSubtree, NodeValue, RightSubtree). Beyond that, there is fairly wide latitude in the tree implementation. Here we'll use a class-based approach:
· BinaryTree is a header object, which initializes and manages the actual tree.
· EmptyNode is the empty object, shared at all empty subtrees (at the bottom).
· BinaryNode objects are nonempty tree nodes with a value and two subtrees.
Rather than coding distinct search functions, binary trees are constructed with "smart" objects (class instances) that know how to handle insert/lookup and printing requests and pass them to subtree objects. In fact, this is another example of the OOP composition relationship in action: tree nodes embed other tree nodes and pass search requests off to the embedded subtrees. A single empty class instance is shared by all empty subtrees in a binary tree, and inserts replace an EmptyNode with a BinaryNode at the bottom (see Example 17-13).
Example 17-13. PP2E\Dstruct\Classics\btree.py
class BinaryTree:
def __init__(self): self.tree = EmptyNode( )
def __repr__(self): return `self.tree`
def lookup(self, value): return self.tree.lookup(value)
def insert(self, value): self.tree = self.tree.insert(value)
class EmptyNode:
def __repr__(self): return '*'def lookup(self, value): # fail at the bottom
return 0 def insert(self, value):return BinaryNode(self, value, self) # add new node at bottom
class BinaryNode:
def __init__(self, left, value, right):self.data, self.left, self.right = value, left, right
def lookup(self, value): if self.data == value: return 1 elif self.data > value:return self.left.lookup(value) # look in left
else:return self.right.lookup(value) # look in right
def insert(self, value): if self.data > value:self.left = self.left.insert(value) # grow in left
elif self.data < value:self.right = self.right.insert(value) # grow in right
return self def __repr__(self): return '( %s, %s, %s )' % (`self.left`, `self.data`, `self.right`)
As usual, BinaryTree can contain objects of any type that support the expected interface protocol -- here, > and < comparisons. This includes class instances with the __cmp__ method. Let's experiment with this module's interfaces. The following code stuffs five integers into a new tree, and then searches for values 0...9:
C:\...\PP2E\Dstruct\Classics>python
>>> from btree import BinaryTree
>>> x = BinaryTree( )>>> for i in [3,1,9,2,7]: x.insert(i)...
>>> for i in range(10): print (i, x.lookup(i)),...
(0, 0) (1, 1) (2, 1) (3, 1) (4, 0) (5, 0) (6, 0) (7, 1) (8, 0) (9, 1)
To watch this tree grow, add a print statement after each insert. Tree nodes print themselves as triples, and empty nodes print as *. The result reflects tree nesting:
>>> y = BinaryTree( )>>> y
*
>>> for i in [3,1,9,2,7]:
... y.insert(i); print y...
( *, 3, * )
( ( *, 1, * ), 3, * )
( ( *, 1, * ), 3, ( *, 9, * ) )
( ( *, 1, ( *, 2, * ) ), 3, ( *, 9, * ) )
( ( *, 1, ( *, 2, * ) ), 3, ( ( *, 7, * ), 9, * ) )
At the end of this chapter, we'll see another way to visualize trees in a GUI (which means you're invited to flip ahead now). Node values in this tree object can be any comparable Python object; for instances, here is a tree of strings:
>>> z = BinaryTree( )>>> for c in 'badce': z.insert(c)...
>>> z
( ( *, 'a', * ), 'b', ( ( *, 'c', * ), 'd', ( *, 'e', * ) ) )
>>> z = BinaryTree( )>>> for c in 'abcde': z.insert(c)...
>>> z
( *, 'a', ( *, 'b', ( *, 'c', ( *, 'd', ( *, 'e', * ) ) ) ) )
Notice the last result here: if items inserted into a binary tree are already ordered, then you wind up with a linear structure, and you lose the search-space partitioning magic of binary trees (the tree grows in right branches only). This is a worst-case scenario, and binary trees generally do a good job of dividing up values in practice. But if you are interested in pursuing this topic further, see a data structures text for tree-balancing techniques that automatically keep the tree as dense as possible.
Also note that to keep the code simple, these trees store a value only, and lookups return a 1 or (true or false). In practice, you sometimes may want to store both a key and an associated value (or even more) at each tree node. Example 17-14 shows what such a tree object looks like, for any prospective lumberjacks in the audience.
Example 17-14. PP2E\Dstruct\Classics\btree-keys.py
class KeyedBinaryTree:
def __init__(self): self.tree = EmptyNode( )
def __repr__(self): return `self.tree`
def lookup(self, key): return self.tree.lookup(key)
def insert(self, key, val): self.tree = self.tree.insert(key, val)
class EmptyNode:
def __repr__(self): return '*'def lookup(self, key): # fail at the bottom
return None
def insert(self, key, val):return BinaryNode(self, key, val, self) # add node at bottom
class BinaryNode:
def __init__(self, left, key, val, right):self.key, self.val = key, val
self.left, self.right = left, right def lookup(self, key): if self.key == key: return self.val elif self.key > key:return self.left.lookup(key) # look in left
else:return self.right.lookup(key) # look in right
def insert(self, key, val): if self.key == key: self.val = val elif self.key > key:self.left = self.left.insert(key, val) # grow in left
elif self.key < key:self.right = self.right.insert(key, val) # grow in right
return self def __repr__(self): return ('( %s, %s=%s, %s )' % (`self.left`, `self.key`, `self.val`, `self.right`)) if __name__ == '__main__':
t = KeyedBinaryTree( )
for (key, val) in [('bbb', 1), ('aaa', 2), ('ccc', 3)]: t.insert(key, val) print t print t.lookup('aaa'), t.lookup('ccc')t.insert('ddd', 4)
t.insert('aaa', 5) # changes key's value
print t
And here is this script's self-test code at work; nodes simply have more content this time around:
C:\...\PP2E\Dstruct\Classics>python btree-keys.py
( ( *, 'aaa'=2, * ), 'bbb'=1, ( *, 'ccc'=3, * ) )
2 3
( ( *, 'aaa'=5, * ), 'bbb'=1, ( *, 'ccc'=3, ( *, 'ddd'=4, * ) ) )
17.5 Graph Searching
Many problems can be represented as a graph, which is a set of states with transitions ("arcs") that lead from one state to another. For example, planning a route for a trip is really a graph search problem in disguise -- the states are places you'd like to visit, and the arcs are the transportation links between them.
This section presents simple Python programs that search through a directed, cyclic graph to find the paths between a start state and a goal. Graphs can be more general than trees, because links may point at arbitrary nodes -- even ones already searched (hence the word "cyclic").
The graph used to test searchers in this section is sketched in Figure 17-1. Arrows at the end of arcs indicate valid paths (e.g., A leads to B, E, and G ). The search algorithms will traverse this graph in a depth-first fashion, and trap cycles in order to avoid looping. If you pretend that this is a map, where nodes represent cities, and arcs represent roads, this example will probably seem a bit more meaningful.
Figure 17-1. A directed graph
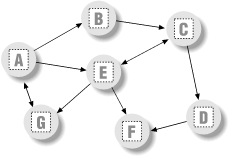
The first thing we need to do is choose a way to represent this graph in a Python script. One approach is to use built-in datatypes and searcher functions. The file in Example 17-15 builds the test graph as a simple dictionary: each state is a dictionary key, with a list of keys of nodes it leads to (i.e., its arcs). This file also defines a function that we'll use to run a few searches in the graph.
Example 17-15. PP2E\Dstruct\Classics\gtestfunc.py
Graph = {'A': ['B', 'E', 'G'],'B': ['C'], # a directed, cyclic graph
'C': ['D', 'E'], # stored as a dictionary
'D': ['F'], # 'key' leads-to [nodes]
'E': ['C', 'F', 'G'],
'F': [ ],
'G': ['A'] }
def tests(searcher): # test searcher functionprint searcher('E', 'D', Graph) # find all paths from 'E' to 'D'
for x in ['AG', 'GF', 'BA', 'DA']: print x, searcher(x[0], x[1], Graph)
Now let's code two modules that implement the actual search algorithms. They are both independent of the graph to be searched (it is passed in as an argument). The first searcher, in Example 17-16, uses recursion to walk through the graph.
Example 17-16. PP2E\Dstruct\Classics\gsearch1.py
# find all paths from start to goal in graph
def search(start, goal, graph):
solns = []
generate([start], goal, solns, graph) # collect paths
solns.sort( lambda x, y: cmp(len(x), len(y)) ) # sort by path length
return solnsdef generate(path, goal, solns, graph):
state = path[-1]if state == goal: # found goal here
solns.append(path) # change solns in-place
else: # check all arcs here
for arc in graph[state]: # skip cycles on path
if arc not in path: generate(path + [arc], goal, solns, graph)if __name__ == '__main__':
import gtestfunc gtestfunc.tests(search)
The second searcher, in Example 17-17, uses an explicit stack of paths to be expanded using the tuple-tree stack representation we explored earlier in this chapter.
Example 17-17. PP2E\Dstruct\Classics\gsearch2.py
# use paths stack instead of recursion
def search(start, goal, graph):
solns = generate( ([start], []), goal, graph) solns.sort( lambda x, y: cmp(len(x), len(y)) )
return solnsdef generate(paths, goal, graph): # returns solns listsolns = [] # use a tuple-stack
while paths:front, paths = paths # pop the top path
state = front[-1] if state == goal:solns.append(front) # goal on this path
else:for arc in graph[state]: # add all extensions
if arc not in front: paths = (front + [arc]), paths return solnsif __name__ == '__main__':
import gtestfunc gtestfunc.tests(search)
Both searchers keep track of nodes visited along a path, to avoid cycles. If an extension is already on the current path, it is a loop. The resulting solutions list is sorted by increasing lengths using the list sort method and the built-in cmp comparison function. To test the searcher modules, simply run them; their self-test code calls the canned search test in the gtestfunc module:
C:\...\PP2E\Dstruct\Classics>python gsearch1.py
[['E', 'C', 'D'], ['E', 'G', 'A', 'B', 'C', 'D']]
AG [['A', 'G'], ['A', 'E', 'G'], ['A', 'B', 'C', 'E', 'G']]
GF [['G', 'A', 'E', 'F'], ['G', 'A', 'B', 'C', 'D', 'F'],
['G', 'A', 'B', 'C', 'E', 'F'], ['G', 'A', 'E', 'C', 'D', 'F']]BA [['B', 'C', 'E', 'G', 'A']]
DA []
C:\...\PP2E\Dstruct\Classics>python gsearch2.py
[['E', 'C', 'D'], ['E', 'G', 'A', 'B', 'C', 'D']]
AG [['A', 'G'], ['A', 'E', 'G'], ['A', 'B', 'C', 'E', 'G']]
GF [['G', 'A', 'E', 'F'], ['G', 'A', 'E', 'C', 'D', 'F'],
['G', 'A', 'B', 'C', 'E', 'F'], ['G', 'A', 'B', 'C', 'D', 'F']]BA [['B', 'C', 'E', 'G', 'A']]
DA []
This output shows lists of possible paths through the test graph; I added two line breaks to make it more readable. Notice that both searchers find the same paths in all tests, but the order in which they find those solutions may differ. The gsearch2 order depends on how and when extensions are added to its path's stack.
17.5.1 Moving Graphs to Classes
Using dictionaries to represent graphs is efficient: connected nodes are located by a fast hashing operation. But depending on the application, other representations might make more sense. For instance, classes can be used to model nodes in a network, too, much like the binary tree example earlier. As classes, nodes may contain content useful for more sophisticated searches. To illustrate, Example 17-18 shows an alternative coding for our graph searcher; its algorithm is closest to gsearch1.
Example 17-18. PP2E\Dstruct\Classics\graph.py
# build graph with objects that know how to search
class Graph:
def __init__(self, label, extra=None):self.name = label # nodes=inst objects
self.data = extra # graph=linked objs
self.arcs = [] def __repr__(self): return self.name def search(self, goal): Graph.solns = []self.generate([self], goal)
Graph.solns.sort(lambda x,y: cmp(len(x), len(y))) return Graph.solns def generate(self, path, goal):if self == goal: # class == tests addr
Graph.solns.append(path) # or self.solns: same
else: for arc in self.arcs: if arc not in path: arc.generate(path + [arc], goal)if __name__ == '__main__':
import gtestobj1 gtestobj1.tests(Graph)
In this version, graphs are represented as a network of embedded class instance objects. Each node in the graph contains a list of the node objects it leads to (arcs), which it knows how to search. The generate method walks through the objects in the graph. But this time, links are directly available on each node's arcs list; there is no need to index (or pass) a dictionary to find linked objects.
To test, the module in Example 17-19 builds the test graph again, this time using linked instances of the Graph class. Notice the use of exec in the self-test code: it executes dynamically constructed strings to do the work of seven assignment statements (A=Graph('A'), B=Graph('B'), etc.).
Example 17-19. PP2E\Dstruct\Classics\gtestobj1.py
def tests(Graph):
for name in "ABCDEFG": # make objects first
exec "%s = Graph('%s')" % (name, name) # label=variable-name
A.arcs = [B, E, G]B.arcs = [C] # now configure their links:
C.arcs = [D, E] # embedded class-instance list
D.arcs = [F] E.arcs = [C, F, G] G.arcs = [A] A.search(G) for (start, stop) in [(E,D), (A,G), (G,F), (B,A), (D,A)]: print start.search(stop)
You run this test by running the graph module to pass in a graph class, like this:
C:\...\PP2E\Dstruct\Classics>python graph.py
[[E, C, D], [E, G, A, B, C, D]]
[[A, G], [A, E, G], [A, B, C, E, G]]
[[G, A, E, F], [G, A, B, C, D, F], [G, A, B, C, E, F], [G, A, E, C, D, F]]
[[B, C, E, G, A]]
[]
The results are the same as for the functions, but node name labels are not quoted: nodes on path lists here are Graph instances, and this class's __repr__ scheme suppresses quotes. Example 17-20 is one last graph test before we move on; sketch the nodes and arcs on paper if you have more trouble following the paths than Python.
Example 17-20. PP2E\Dstruct\Classics\gtestobj2.py
from graph import Graph
S = Graph('s')P = Graph('p') # a graph of spamA = Graph('a') # make node objectsM = Graph('m') S.arcs = [P, M] # S leads to P and MP.arcs = [S, M, A] # arcs: embedded objectsA.arcs = [M]
print S.search(M) # find all paths from S to M
This test finds three paths in its graph between nodes S and M. If you'd like to see more Python graph code, check out the files in directory MoreGraphs on the CD (see http://examples.oreilly.com/python2). These are roughly the same as the ones listed here, but add user interaction as each solution is found. In addition, we've really only scratched the surface of this domain here; see other books for additional topics (e.g., breadth- and best-first search):
C:\...\PP2E\Dstruct\Classics>python gtestobj2.py
[[s, m], [s, p, m], [s, p, a, m]]
17.6 Reversing Sequences
Reversal of collections is another typical operation. We can code it either recursively or iteratively in Python, and as functions or class methods. Example 17-21 is a first attempt at two simple reversal functions.
Example 17-21. PP2E\Dstruct\Classics\rev1.py
def reverse(list): # recursive if list == []: return [] else: return reverse(list[1:]) + list[:1]def ireverse(list): # iterative res = [] for x in list: res = [x] + res return res
Both reversal functions work correctly on lists. But if we try reversing nonlist sequences (strings, tuples, etc.) we're in trouble: the ireverse function always returns a list for the result regardless of the type of sequence passed:
>>> ireverse("spam")['m', 'a', 'p', 's']
Much worse, the recursive reverse version won't work at all for nonlists -- it gets stuck in an infinite loop. The reason is subtle: when reverse reaches the empty string (""), it's not equal to the empty list ([]), so the else clause is selected. But slicing an empty sequence returns another empty sequence (indexes are scaled): the else clause recurs again with an empty sequence, and without raising an exception. The net effect is that this function gets stuck in a loop, calling itself over and over again until Python runs out of memory.
The versions in Example 17-22 fix both problems by using generic sequence handling techniques:
· reverse uses the not operator to detect the end of the sequence and returns the empty sequence itself, rather than an empty list constant. Since the empty sequence is the type of the original argument, the + operation always builds the correct type sequence as the recursion unfolds.
· ireverse makes use of the fact that slicing a sequence returns a sequence of the same type. It first initializes the result to the slice [:0], a new, empty slice of the argument's type. Later, it uses slicing to extract one-node sequences to add to the result's front, instead of a list constant.
Example 17-22. PP2E\Dstruct\Classics\rev2.py
def reverse(list):
if not list: # empty? (not always [])
return list # the same sequence type
else:return reverse(list[1:]) + list[:1] # add front item on the end
def ireverse(list):
res = list[:0] # empty, of same type
for i in range(len(list)): res = list[i:i+1] + res # add each item to front
return res
These functions work on any sequence, and return a new sequence of the same type as the sequence passed in. If we pass in a string, we get a new string as the result. In fact, they reverse any sequence object that responds to slicing, concatenation, and len -- even instances of Python classes and C types. In other words, they can reverse any object that has sequence interface protocols. Here they are working on lists, strings, and tuples:
% python
>>> from rev2 import *
>>> reverse([1,2,3]), ireverse([1,2,3])
([3, 2, 1], [3, 2, 1])
>>> reverse("spam"), ireverse("spam")('maps', 'maps')>>> reverse((1.2, 2.3, 3.4)), ireverse((1.2, 2.3, 3.4))
((3.4, 2.3, 1.2), (3.4, 2.3, 1.2))
17.7 Permuting Sequences
The functions defined in Example 17-23 shuffle sequences in a number of ways:
· permute constructs a list with all valid permutations of any sequence.
· subset constructs a list with all valid permutations of a specific length.
· combo works like subset, but order doesn't matter: permutations of the same items are filtered out.
These results are useful in a variety of algorithms: searches, statistical analysis, and more. For instance, one way to find an optimal ordering for items is to put them in a list, generate all possible permutations, and simply test each one in turn. All three of the functions make use of the generic sequence slicing tricks of the reversal functions in the prior section, so that the result list contains sequences of the same type as the one passed in (e.g., when we permute a string, we get back a list of strings).
Example 17-23. PP2E\Dstruct\Classics\permcomb.py
def permute(list):
if not list: # shuffle any sequence
return [list] # empty sequence
else: res = [] for i in range(len(list)):rest = list[:i] + list[i+1:] # delete current node
for x in permute(rest): # permute the others
res.append(list[i:i+1] + x) # add node at front
return resdef subset(list, size):
if size == 0 or not list: # order matters here
return [list[:0]] # an empty sequence
else: result = [] for i in range(len(list)):pick = list[i:i+1] # sequence slice
rest = list[:i] + list[i+1:] # keep [:i] part
for x in subset(rest, size-1): result.append(pick + x) return resultdef combo(list, size):
if size == 0 or not list: # order doesn't matter
return [list[:0]] # xyz == yzx
else: result = []for i in range(0, (len(list) - size) + 1): # iff enough left
pick = list[i:i+1] rest = list[i+1:] # drop [:i] part
for x in combo(rest, size - 1): result.append(pick + x) return result
As in the reversal functions, all three of these work on any sequence object that supports len, slicing, and concatenation operations. For instance, we can use permute on instances of some of the stack classes defined at the start of this chapter; we'll get back a list of stack instance objects with shuffled nodes.
Here are our sequence shufflers in action. Permuting a list enables us to find all the ways the items can be arranged. For instance, for a four-item list, there are 24 possible permutations (4 x 3 x 2 x 1). After picking one of the four for the first position, there are only three left to choose from for the second, and so on. Order matters: [1,2,3] is not the same as [1,3,2], so both appear in the result:
C:\...\PP2E\Dstruct\Classics>python
>>> from permcomb import *
>>> permute([1,2,3])
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
>>> permute('abc')['abc', 'acb', 'bac', 'bca', 'cab', 'cba']
>>> permute('help')['help', 'hepl', 'hlep', 'hlpe', 'hpel', 'hple', 'ehlp', 'ehpl', 'elhp', 'elph',
'ephl', 'eplh', 'lhep', 'lhpe', 'lehp', 'leph', 'lphe', 'lpeh', 'phel', 'phle',
'pehl', 'pelh', 'plhe', 'pleh']
combo results are related to permutations, but a fixed-length constraint is put on the result, and order doesn't matter: abc is the same as acb, so only one is added to the result set:
>>> combo([1,2,3], 3)
[[1, 2, 3]]
>>> combo('abc', 3)['abc']
>>> combo('abc', 2)['ab', 'ac', 'bc']
>>> combo('abc', 4)[]
>>> combo((1, 2, 3, 4), 3)
[(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4)]
>>> for i in range(0, 6): print i, combo("help", i)...
0 ['']
1 ['h', 'e', 'l', 'p']
2 ['he', 'hl', 'hp', 'el', 'ep', 'lp']
3 ['hel', 'hep', 'hlp', 'elp']
4 ['help']
5 []
Finally, subset is just fixed-length permutations; order matters, so the result is larger than for combo. In fact, calling subset with the length of the sequence is identical to permute:
>>> subset([1,2,3], 3)
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
>>> subset('abc', 3)['abc', 'acb', 'bac', 'bca', 'cab', 'cba']
>>> for i in range(0, 6): print i, subset("help", i)...
0 ['']
1 ['h', 'e', 'l', 'p']
2 ['he', 'hl', 'hp', 'eh', 'el', 'ep', 'lh', 'le', 'lp', 'ph', 'pe', 'pl']
3 ['hel', 'hep', 'hle', 'hlp', 'hpe', 'hpl', 'ehl', 'ehp', 'elh', 'elp', 'eph',
'epl', 'lhe', 'lhp', 'leh', 'lep', 'lph', 'lpe', 'phe', 'phl', 'peh', 'pel', 'plh', 'ple']4 ['help', 'hepl', 'hlep', 'hlpe', 'hpel', 'hple', 'ehlp', 'ehpl', 'elhp',
'elph', 'ephl', 'eplh', 'lhep', 'lhpe', 'lehp', 'leph', 'lphe', 'lpeh', 'phel', 'phle', 'pehl', 'pelh', 'plhe', 'pleh']5 ['help', 'hepl', 'hlep', 'hlpe', 'hpel', 'hple', 'ehlp', 'ehpl', 'elhp',
'elph', 'ephl', 'eplh', 'lhep', 'lhpe', 'lehp', 'leph', 'lphe', 'lpeh', 'phel', 'phle', 'pehl', 'pelh', 'plhe', 'pleh']
17.8 Sorting Sequences
Another staple of many systems is sorting: ordering items in a collection according to some constraint. The script in Example 17-24 defines a simple sort routine in Python, which orders a list of objects on a field. Because Python indexing is generic, the field can be an index or key -- this function can sort lists of either sequences or mappings.
Example 17-24. PP2E\Dstruct\Classics\sort1.py
def sort(list, field):
res = [] # always returns a list
for x in list: i = 0 for y in res:if x[field] <= y[field]: break # list node goes here?
i = i+1res[i:i] = [x] # insert in result slot
return res if __name__ == '__main__':
table = [ {'name':'john', 'age':25}, {'name':'doe', 'age':32} ] print sort(table, 'name') print sort(table, 'age')
table = [ ('john', 25), ('doe', 32) ] print sort(table, 0) print sort(table, 1)
Here is this module's self-test code in action:
C:\...\PP2E\Dstruct\Classics>python sort1.py
[{'age': 32, 'name': 'doe'}, {'age': 25, 'name': 'john'}][{'age': 25, 'name': 'john'}, {'age': 32, 'name': 'doe'}][('doe', 32), ('john', 25)][('john', 25), ('doe', 32)]
17.8.1 Adding Comparison Functions
Since functions can be passed in like any other object, we can easily allow for an optional comparison function. In the next version (Example 17-25), the second argument takes a function that should return true if its first argument should be placed before its second. A lambda is used to provide an ascending-order test by default. This sorter also returns a new sequence that is the same type as the sequence passed in, by applying the slicing techniques used in earlier sections: if you sort a tuple of nodes, you get back a tuple.
Example 17-25. PP2E\Dstruct\Classics\sort2.py
def sort(seq, func=(lambda x,y: x <= y)): # default: ascendingres = seq[:0] # return seq's type
for j in range(len(seq)): i = 0 for y in res: if func(seq[j], y): break i = i+1res = res[:i] + seq[j:j+1] + res[i:] # seq can be immutable
return res if __name__ == '__main__':
table = ({'name':'doe'}, {'name':'john'})print sort(list(table), (lambda x, y: x['name'] > y['name']))
print sort(tuple(table), (lambda x, y: x['name'] <= y['name'])) print sort('axbyzc')
This time, the table entries are ordered per a field comparison function passed in:
C:\...\PP2E\Dstruct\Classics>python sort2.py
[{'name': 'john'}, {'name': 'doe'}]({'name': 'doe'}, {'name': 'john'})abcxyz
This version also dispenses with the notion of a field altogether and lets the passed-in function handle indexing if needed. That makes this version much more general; for instance, it's also useful for sorting strings.
17.9 Data Structures Versus Python Built-ins
Now that I've shown you all these complicated algorithms, I need to also tell you that at least in some cases, they may not be an optimal approach. Built-in types like lists and dictionaries are often a simpler and more efficient way to represent data. For instance:
Binary trees
These may be useful in many applications, but Python dictionaries already provide a highly optimized, C-coded, search table tool. Indexing a dictionary by key is likely to be faster than searching a Python-coded tree structure:
>>> x = {}>>> for i in [3,1,9,2,7]: x[i] = None # insert>>> for i in range(10): print (i, x.has_key(i)), # lookup(0, 0) (1, 1) (2, 1) (3, 1) (4, 0) (5, 0) (6, 0) (7, 1) (8, 0) (9, 1)
Because dictionaries are built in to the language, they are always available, and will usually be faster than Python-based data structure implementations.
Graph algorithms
These serve many purposes, but a purely Python-coded implementation of a very large graph might be less efficient than you want in some applications. Graph programs tend to require peak performance; using dictionaries instead of class instances to represent graphs may boost performance some, but using linked-in compiled extensions may as well.
Sorting algorithms
These are an important part of many programs too, but Python's built-in list sort method is so fast that you would be hard pressed to beat it in Python in most scenarios. In fact, it's generally better to convert sequences to lists first just so you can use the built-in:
temp = list(sequence)
temp.sort( )...use items in temp...
For custom sorts, simply pass in a comparison function of your own:
>>> L = [{'n':3}, {'n':20}, {'n':0}, {'n':9}] >>> L.sort( lambda x, y: cmp(x['n'], y['n']) ) >>> L
[{'n': 0}, {'n': 3}, {'n': 9}, {'n': 20}]
Reversal algorithms
These are generally superfluous by the same token -- because Python lists provide a fast reverse method, you may be better off converting a non-list to a list first, just so that you can run the built-in list method.
Don't misunderstand: sometimes you really do need objects that add functionality to built-in types, or do something more custom. The set classes we met, for instance, add tools not directly supported by Python today, and the tuple-tree stack implementation was actually faster than one based upon built-in lists for common usage patterns. Permutations are something you need to add on your own too.
Moreover, class encapsulations make it possible to change and extend object internals without impacting the rest of your system. They also support reuse much better than built-in types -- types are not classes today, and cannot be specialized directly without wrapper class logic.
Yet because Python comes with a set of built-in, flexible, and optimized datatypes, data structure implementations are often not as important in Python as they are in lesser-equipped languages such as C or C++. Before you code that new datatype, be sure to ask yourself if a built-in type or call might be more in line with the Python way of thinking.
17.10 PyTree: A Generic Tree Object Viewer
Up to now, this chapter has been command-line-oriented. To wrap up, I want to show you a program that merges the GUI technology we studied earlier in the book with some of the data structure ideas we've met in this chapter.
This program is called PyTree, a generic tree data structure viewer written in Python with the Tkinter GUI library. PyTree sketches out the nodes of a tree on screen as boxes connected by arrows. It also knows how to route mouseclicks on drawn tree nodes back to the tree, to trigger tree-specific actions. Because PyTree lets you visualize the structure of the tree generated by a set of parameters, it's a fun way explore tree-based algorithms.
PyTree supports arbitrary tree types by "wrapping" real trees in interface objects. The interface objects implement a standard protocol by communicating with the underlying tree object. For the purposes of this chapter, PyTree is instrumented to display binary search trees ; for the next chapter, it's also set up to render expression parse trees. New trees can be viewed by coding wrapper classes to interface to new tree types.
The GUI interfaces PyTree utilizes were covered in depth earlier in this book, so I won't go over this code in much detail here. See Part II, for background details, and be sure to run this program on your own computer to get a better feel for its operation. Because it is written with Python and Tkinter, it should be portable to Windows, Unix, and Macs.
17.10.1 Running PyTree
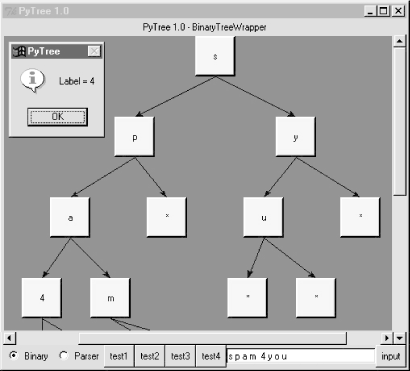
Before we get to the code, let's see what PyTree looks like. You can launch PyTree from the PyDemos launcher bar (see the top-level of the examples distribution source tree at http://examples.oreilly.com/python2), or by directly running the treeview.py file listed in Example 17-27. Figure 17-2 shows PyTree in action displaying the binary tree created by the "test1" button. Trees are sketched as labels embedded in a canvas, and connected by lines with arrows. The lines reflect parent-to-child relationships in the actual tree; PyTree attempts to layout the tree to produce a more or less uniform display like this one.
Figure 17-2. PyTree viewing a binary search tree (test1)

PyTree's window consists of a canvas with vertical and horizontal scrolls, and a set of controls at the bottom -- radiobuttons for picking the type of tree you wish to display, a set of buttons that trigger canned tree drawing tests, and an input field for typing text to specify and generate a new tree. The set of test buttons changes if you pick the Parser radiobutton (you get one less test button); PyTree use widget pack_forget and pack methods to hide and show tree-specific buttons on the fly.
When you pick one of the canned test buttons, it displays in the input field the string you would type to generate the tree drawn. For binary trees, type a list of values separated by spaces and press the "input" button or the Enter key to generate a new tree; the new tree is the result of inserting the typed values from left to right. For parse trees, you input an expression string in the input field instead (more on this later). Figure 17-3 shows the result of typing a set of values into the input field and submitting; the resulting binary tree shows up in the canvas.
Figure 17-3. A binary tree typed manually with on-click pop-up
Notice the pop-up in this screen shot; left-clicking on a displayed tree node with your mouse runs whatever action a tree wrapper class defines, and displays its result in the pop-up. Binary trees have no action to run, so we get a default message in the pop-up, but parse tress use the mouseclick to evaluate the subtree rooted at the clicked node (again, more on parse trees later).
Just for fun, maximize this window and press the "test4" button -- it inserts 100 numbers from through 99 into a new binary tree at random, and displays the result. Figure 17-4 captures one portion of this tree; it's much too large to fit on one screen (or on one book page), but you can move around the tree with the canvas scrollbars.
Figure 17-4. PyTree viewing a large binary search tree (test4)

PyTree uses an algorithm to connect all parents to their children in this tree without crossing their connecting lines. It does some up-front analysis to try and arrange descendents at each level to be as close to their parents as possible. This analysis step also yields the overall size of a new tree -- PyTree uses it to reset the scrollable area size of the canvas for each tree drawn.
17.10.2 Pytree Source Code
Let's move on to the code. Similar to PyForm in the prior chapter, PyTree is coded as two modules; here, one module handles the task of sketching trees in the GUI, and another implements wrappers to interface to various tree types and extends the GUI with extra widgets.
17.10.2.1 Tree-independent GUI implementation
The module in Example 17-26 does the work of drawing trees in a canvas. It's coded to be independent of any particular tree structure -- its TreeViewer class delegates to its TreeWrapper class when it needs tree-specific information for the drawing (e.g., node label text, node child links). TreeWrapper in turn expects to be subclassed for a specific kind of tree; in fact it raises assertion errors if you try to use it without subclassing. In design terms, TreeViewer embeds a TreeWrapper; it's almost as easy to code TreeViewer subclasses per tree type, but that limits a viewer GUI to one particular kind of tree (see treeview_subclasses.py at http://examples.oreilly.com/python2 for a subclassing-based alternative).
Trees are drawn in two steps -- a planning traversal the builds a layout data structure that links parents and children, and a drawing step that uses the generated plan to draw and link node labels on the canvas. The two-step approach simplifies some of the logic required to layout trees uniformly. Study this listing for more details.
Example 17-26. PP2E\Dstruct\TreeView\treeview_wrappers.py
#########################################################################
# PyTree: sketch arbitrary tree data structures in a scrolled canvas;
# this version uses tree wrapper classes embedded in the viewer gui
# to support arbitrary trees (i.e.. composition, not viewer subclassing);
# also adds tree node label click callbacks--run tree specific actions;
# see treeview_subclasses.py for subclass-based alternative structure;
# subclassing limits one tree viewer to one tree type, wrappers do not;
# see treeview_left.py for an alternative way to draw the tree object;
# see and run treeview.py for binary and parse tree wrapper test cases;
#########################################################################
from Tkinter import *
from tkMessageBox import showinfo
Width, Height = 350, 350 # start canvas size (reset per tree)Rowsz = 100 # pixels per tree rowColsz = 100 # pixels per tree col###################################
# interface to tree object's nodes
###################################
class TreeWrapper: # subclass for a tree type def children(self, treenode): assert 0, 'children method must be specialized for tree type' def label(self, treenode): assert 0, 'label method must be specialized for tree type' def value(self, treenode): return ''def onClick(self, treenode): # node label click callback
return ''def onInputLine(self, line, viewer): # input line sent callback
pass###########$######################
# tree view gui, tree independent
##################################
class TreeViewer(Frame):
def __init__(self, wrapper, parent=None, tree=None, bg='brown', fg='beige'): Frame.__init__(self, parent) self.pack(expand=YES, fill=BOTH)self.makeWidgets(bg) # build gui: scrolled canvas
self.master.title('PyTree 1.0') # assume I'm run standalone
self.wrapper = wrapper # embed a TreeWrapper object
self.fg = fg # setTreeType changes wrapper
if tree: self.drawTree(tree) def makeWidgets(self, bg): self.title = Label(self, text='PyTree 1.0') self.canvas = Canvas(self, bg=bg, borderwidth=0) vbar = Scrollbar(self) hbar = Scrollbar(self, orient='horizontal') self.title.pack(side=TOP, fill=X)vbar.pack(side=RIGHT, fill=Y) # pack canvas after bars
hbar.pack(side=BOTTOM, fill=X) self.canvas.pack(side=TOP, fill=BOTH, expand=YES)vbar.config(command=self.canvas.yview) # call on scroll move
hbar.config(command=self.canvas.xview)self.canvas.config(yscrollcommand=vbar.set) # call on canvas move
self.canvas.config(xscrollcommand=hbar.set)self.canvas.config(height=Height, width=Width) # viewable area size
def clearTree(self):mylabel = 'PyTree 1.0 - ' + self.wrapper.__class__.__name__
self.title.config(text=mylabel) self.unbind_all('<Button-1>')self.canvas.delete('all') # clear events, drawing
def drawTree(self, tree):self.clearTree( )
wrapper = self.wrapper levels, maxrow = self.planLevels(tree, wrapper)self.canvas.config(scrollregion=( # scrollable area
0, 0, (Colsz * maxrow), (Rowsz * len(levels)) )) # upleft, lowright
self.drawLevels(levels, maxrow, wrapper) def planLevels(self, root, wrap): levels = []maxrow = 0 # traverse tree to
currlevel = [(root, None)] # layout rows, cols
while currlevel: levels.append(currlevel) size = len(currlevel) if size > maxrow: maxrow = size nextlevel = [] for (node, parent) in currlevel: if node != None:children = wrap.children(node) # list of nodes
if not children:nextlevel.append((None, None)) # leave a hole
else:for child in children:
nextlevel.append((child, node)) # parent link
currlevel = nextlevel return levels, maxrow def drawLevels(self, levels, maxrow, wrap):rowpos = 0 # draw tree per plan
for level in levels: # set click handlers
colinc = (maxrow * Colsz) / (len(level) + 1) # levels is treenodes
colpos = 0 for (node, parent) in level: colpos = colpos + colinc if node != None: text = wrap.label(node) more = wrap.value(node) if more: text = text + '=' + more win = Label(self.canvas, text=text, bg=self.fg, bd=3, relief=RAISED)win.pack( )
win.bind('<Button-1>', lambda e, n=node, handler=self.onClick: handler(e, n)) self.canvas.create_window(colpos, rowpos, anchor=NW, window=win, width=Colsz*.5, height=Rowsz*.5) if parent != None: self.canvas.create_line(parent.__colpos + Colsz*.25, # from x-y, to x-y
parent.__rowpos + Rowsz*.5, colpos + Colsz*.25, rowpos, arrow='last', width=1) node.__rowpos = rowposnode.__colpos = colpos # mark node, private attrs
rowpos = rowpos + Rowsz def onClick(self, event, node): label = event.widgetwrap = self.wrapper
text = 'Label = ' + wrap.label(node) # on label click
value = wrap.value(node) if value: text = text + '\nValue = ' + value # add tree text if any
result = wrap.onClick(node) # run tree action if any
if result:text = text + '\n' + result # add action result
showinfo('PyTree', text) # popup std dialog
def onInputLine(self, line): # feed text to tree wrapper
self.wrapper.onInputLine(line, self) # ex: parse and redraw tree
def setTreeType(self, newTreeWrapper): # change tree type drawn
if self.wrapper != newTreeWrapper: # effective on next draw
self.wrapper = newTreeWrapperself.clearTree( ) # else old node, new wrapper
17.10.2.2 Tree wrappers and test widgets
The other half of PyTree consists of a module that defines TreeWrapper subclasses that interface to binary and parser trees, implements canned test case buttons, and adds the control widgets to the bottom of the PyTree window.[4] These control widgets were split off into this separate module (in Example 17-27) on purpose, because the PyTree canvas might be useful as a viewer component in other GUI applications.
Example 17-27. PP2E\Dstruct\TreeView\treeview.py
# PyTree launcher script
# wrappers for viewing tree types in the book, plus test cases/gui
import string
from Tkinter import *
from treeview_wrappers import TreeWrapper, TreeViewer
from PP2E.Dstruct.Classics import btree
from PP2E.Lang.Parser import parser2
###################################################################
# binary tree wrapper
###################################################################
class BinaryTreeWrapper(TreeWrapper): # embed binary tree in viewerdef children(self, node): # adds viewer protocols
try: # to interface with tree
return [node.left, node.right] except: return None def label(self, node):try:
return str(node.data)
except: return str(node)def onInputLine(self, line, viewer): # on test entry at bottom
items = string.split(line) # make tree from text input
t = btree.BinaryTree( ) # draw resulting btree
for x in items: t.insert(x) # no onClick handler here
viewer.drawTree(t.tree)###################################################################
# binary tree extension
###################################################################
class BinaryTree(btree.BinaryTree):
def __init__(self, viewer): # embed viewer in tree
btree.BinaryTree.__init__(self) # but viewer has a wrapper
self.viewer = viewer
def view(self): self.viewer.drawTree(self.tree)###################################################################
# parse tree wrapper
###################################################################
class ParseTreeWrapper(TreeWrapper):
def __init__(self): # embed parse tree in viewer
self.dict = {} # adds viewer protocols
def children(self, node): try: return [node.left, node.right] except: try: return [node.var, node.val] except: return None def label(self, node): for attr in ['label', 'num', 'name']: if hasattr(node, attr): return str(getattr(node, attr)) return 'set'def onClick(self, node): # on tree label click
try: # tree-specific action
result = node.apply(self.dict) # evaluate subtree
return 'Value = ' + str(result) # show result in popup
except: return 'Value = <error>'def onInputLine(self, line, viewer): # on input line
p = parser2.Parser( ) # parse expr text
p.lex.newtext(line) # draw resulting tree
t = p.analyse( )
if t: viewer.drawTree(t)###################################################################
# canned test cases (or type new nodelists/exprs in input field)
###################################################################
def shownodes(sequence):
sequence = map(str, sequence) # convert nodes to strings
entry.delete(0, END) # show nodes in text field
entry.insert(0, string.join(sequence, ' '))def test1_binary( ): # tree type is binary wrapper
nodes = [3, 1, 9, 2, 7] # make a binary tree
tree = BinaryTree(viewer) # embed viewer in tree
for i in nodes: tree.insert(i)
shownodes(nodes) # show nodes in input field
tree.view( ) # sketch tree via embedded viewer
def test2_binary( ): nodes = 'badce'tree = btree.BinaryTree( ) # embed wrapper in viewer
for c in nodes: tree.insert(c) # make a binary tree
shownodes(nodes)viewer.drawTree(tree.tree) # ask viewer to draw it
def test3_binary( ): nodes = 'abcde'tree = BinaryTree(viewer)
for c in nodes: tree.insert(c) shownodes(nodes)tree.view( )
def test4_binary( ): tree = BinaryTree(viewer)import random # make a big binary tree
nodes = range(100) # insert 100 nodes at random
order = [] # and sketch in viewer
while nodes: item = random.choice(nodes) nodes.remove(item) tree.insert(item) order.append(item) shownodes(order)tree.view( )
def test_parser(expr):
parser = parser2.Parser( ) # tree type is parser wrapper
parser.lex.newtext(expr) # subtrees evaluate when clicked
tree = parser.analyse( ) # input line parses new expr
entry.delete(0, END) # vars set in wrapper dictionary
entry.insert(0, expr) # see lang/text chapter for parser
if tree: viewer.drawTree(tree)def test1_parser( ): test_parser("1 + 3 * (2 * 3 + 4)")
def test2_parser( ): test_parser("set temp 1 + 3 * 2 * 3 + 4")def test3_parser( ): test_parser("set result temp + ((1 + 3) * 2) * (3 + 4)")###################################################################
# build viewer with extra widgets to test tree types
###################################################################
if __name__ == '__main__':
root = Tk( ) # build a single viewer gui
bwrapper = BinaryTreeWrapper( ) # add extras: input line, test btns
pwrapper = ParseTreeWrapper( ) # make wrapper objects
viewer = TreeViewer(bwrapper, root) # start out in binary mode
def onRadio( ):
if var.get( ) == 'btree':
viewer.setTreeType(bwrapper) # change viewer's wrapper
for btn in p_btns: btn.pack_forget( ) # erase parser test buttons
for btn in b_btns: btn.pack(side=LEFT) # unhide binary buttons
elif var.get( ) == 'ptree':
viewer.setTreeType(pwrapper)for btn in b_btns: btn.pack_forget( )
for btn in p_btns: btn.pack(side=LEFT)var = StringVar( )
var.set('btree') Radiobutton(root, text='Binary', command=onRadio, variable=var, value='btree').pack(side=LEFT) Radiobutton(root, text='Parser', command=onRadio, variable=var, value='ptree').pack(side=LEFT) b_btns = [] b_btns.append(Button(root, text='test1', command=test1_binary)) b_btns.append(Button(root, text='test2', command=test2_binary)) b_btns.append(Button(root, text='test3', command=test3_binary)) b_btns.append(Button(root, text='test4', command=test4_binary)) p_btns = [] p_btns.append(Button(root, text='test1', command=test1_parser)) p_btns.append(Button(root, text='test2', command=test2_parser)) p_btns.append(Button(root, text='test3', command=test3_parser))onRadio( )
def onInputLine( ):
line = entry.get( ) # use per current tree wrapper type
viewer.onInputLine(line) # type a node list or expression
Button(root, text='input', command=onInputLine).pack(side=RIGHT) entry = Entry(root) entry.pack(side=RIGHT, expand=YES, fill=X)entry.bind('<Return>', lambda event: onInputLine( )) # button or enter key
root.mainloop( ) # start up the gui
17.10.3 Pytree Does Parse Trees, Too
Finally, I want to show you what happens when you click the Parser radiobutton in the PyTree window. The GUI changes over to an expression parse tree viewer, by simply using a different tree wrapper class: the label at the top changes, the test buttons change, and input is now entered as an arithmetic expression to be parsed and sketched. Figure 17-5 shows a tree generated for the expression string displayed in the input field.
Figure 17-5. PyTree viewing an expression parse tree

PyTree is designed to be generic -- it displays both binary and parse trees, but is easy to extend for new tree types with new wrapper classes. On the GUI, you can switch between binary and parser tree types at any time by clicking the radiobuttons. Input typed into the input field is always evaluated according to the current tree type. When the viewer is in parse tree mode, clicking on a node in the tree evaluates the part of the expression represented by the parse tree rooted at the node you clicked. Figure 17-6 shows the pop-up you get when you click the root node of the tree displayed.
Figure 17-6. PyTree pop-up after clicking a parse tree node

When viewing parse trees, PyTree becomes a sort of visual calculator -- you can generate arbitrary expression trees and evaluate any part of them by clicking on nodes displayed. But at this point, there is not much more I can tell you about these kinds of trees until you move on to Chapter 18.
[1] In fact, Python 1.5 introduced a list pop method designed to be used in conjunction with append to implement stacks: to push, say list.append(value), to pop, say x=list.pop( ). The pop method
is equivalent to fetching and then deleting the last item at offset -1 (and
equal to the last row in column 2 of Table 17-1). Because lists are a type (not
a class), though, you still may need to use the stack class techniques in this
chapter to do something custom. [back]
[2] If you have a copy of the first edition of this book
lying around, you might notice that I had to scale all test factors way up to
get even close to the run times I noticed before. Both Python and chips have
gotten a lot faster in five years. [back]
[3] If you're looking for a more graphical image of binary
trees, skip ahead to the PyTreeexamples at the end of this chapter, or simply
run it on your own machine. [back]
[4] If you're looking for a coding exercise, try adding
another wrapper class and radiobutton to view the KeyedBinaryTree we wrote earlier in this chapter. You'll probably want
to display the key in the GUI, and pop up the associated value on clicks. [back]
Chapter 16 TOC Chapter 18