13.1.1 The ABS function

The ABS function returns the absolute value of the input. The specification for the ABS function is:

FUNCTION ABS (n NUMBER) RETURN NUMBER;

The ABS function can help simplify your code logic. Here's an example:

In one program I reviewed, line items and amounts for a profit and loss statement were footed or balanced. If the variance on the line amount was greater than $100, either positive or negative, that line item was flagged as "in error." The first version of the code that implemented this requirement looked like this (variance_table is a PL/SQL table holding the variance for each line item):

IF variance_table (line_item_nu) BETWEEN 1 AND 100 OR
   variance_table (line_item_nu) BETWEEN -100 AND -1
THEN
   apply_variance (statement_id);
ELSE
   flag_error (statement_id, line_item_nu);
END IF;

There are two ways to express this logic. First, do not hardcode the maximum allowable variance; put the value in a named constant. Second, use ABS so that you perform the range check only once. With these changes, the above code can be rewritten as follows:

IF ABS (variance_table (line_item_nu))
   BETWEEN min_variance AND max_variance
THEN
   apply_variance (statement_id);
ELSE
   flag_error (statement_id, line_item_nu);
END IF;

13.1.2 The ACOS function

The ACOS function returns the inverse cosine. The specification for the ACOS function is:

FUNCTION ACOS (n NUMBER) RETURN NUMBER;

where the number n must be between -1 and 1, and the value returned by ACOS is between 0 and pi.

13.1.3 The ASIN function

The ASIN function returns the inverse sine. The specification for the ASIN function is:

FUNCTION ASIN (n NUMBER) RETURN NUMBER;

where the number n must be between -1 and 1, and the value returned by ASIN is between -pi/2 and pi/2.

13.1.4 The ATAN function

The ATAN function returns the inverse tangent. The specification for the ATAN function is:

FUNCTION ATAN (n NUMBER) RETURN NUMBER;

where the number n must be between -infinity and infinity, and the value returned by ATAN is between -pi/2 and pi/2.

13.1.5 The ATAN2 function

The ATAN2 function returns the result of the tan2 inverse trigonometric function. The specification for the ATAN2 function is:

FUNCTION ATAN (n NUMBER, m NUMBER) RETURN NUMBER;

where the numbers n and m must be between -infinity and infinity, and the value returned by ATAN is between -pi and pi.

As a result, the following holds true:

• atan2(-0.00001, -1) is approximately -pi.

• atan2(0,-1) is pi.

13.1.6 The CEIL function

The CEIL ("ceiling") function returns the smallest integer greater than or equal to the specified number. The specification for the CEIL function is:

FUNCTION CEIL (n NUMBER) RETURN NUMBER;

Here are some examples of the effect of CEIL:

CEIL (6) ==> 6
CEIL (119.1) ==> 120
CEIL (-17.2) ==> -17

I have found CEIL useful in calculating loop indexes for date ranges. Suppose that I need to calculate the net profit for sales activity in each month between two dates, and to store each value in a PL/SQL table. I don't really care where in the month the endpoints of the date range fall; I simply want to start from that month and loop through each month in between to the last month.

I could use a WHILE loop which increments a date variable until it is past the end date. That code would look like this:

PROCEDURE fill_profit_table (start_date_in IN DATE, end_date_in IN DATE)
IS
   /* Need local variables for loop condition and row in table. */
   curr_date DATE;
   month_index BINARY_INTEGER;
BEGIN
   /* Use TRUNC to always compare against first days of month. */
   curr_date := TRUNC (start_date_in, 'MONTH');
   month_index := 1;

   /* Loop until date exceeds  */
   WHILE curr_date <= TRUNC (end_date_in, 'MONTH')
   LOOP
      profit (month_index) := calc_profits (curr_date, 'NET');
      month_index := month_index + 1;
      curr_date := ADD_MONTHS (curr_date, 1);
   END LOOP;
END;

That works fine, but with CEIL I can produce a much simpler and cleaner implementation, as shown in the following code. I use both CEIL and MONTHS_BETWEEN to compute the number of months over which I need to calculate net profit. This number of months then bexcomes the upper limit of a fixed, numeric FOR loop. For each iteration of that loop, I call the calc_profits function and stuff the return value into the table:

PROCEDURE fill_profit_table (start_date_in IN DATE, end_date_in IN DATE)
IS
   number_of_months INTEGER :=
      CEIL (MONTHS_BETWEEN (end_date_in, start_date_in-1));
BEGIN
   FOR month_index IN 1 .. number_of_months
   LOOP
      profit (month_index) :=
         calc_profits (ADD_MONTHS (start_date_in, month_index - 1), 'NET');
   END LOOP;
END;

Notice that I subtract a day from the start_date_in in my computation of the number of months. I have to do this because if both the start_date_in and the end_date_in fall on the last days of their months, MONTHS_BETWEEN is one less than I need. In other words, if start_date_in = 28-FEB-97 and end_date is 31-MAR-97, MONTHS_BETWEEN (end_date_in, start_date_in) returns 1. For the purposes of this program, however, I need to generate profits for two months.

For a comparison of CEIL with several other numeric functions, see Section 13.1.23, "Rounding and Truncation with PL/SQL" later in this chapter.

13.1.7 The COS function

The COS trigonometric function returns the cosine of the specified angle. The specification for the COS function is:

FUNCTION COS (angle NUMBER) RETURN NUMBER;

where angle must be expressed in radians. A radian is equal to 180/pi or roughly 57.29578. If your angle is specified in degrees, then you should call COS as follows:

my_cosine := COS (angle_in_degrees/57.29578);

13.1.8 The COSH function

The COSH trigonometric function returns the hyperbolic cosine of the specified number. The specification for the COSH function is:

FUNCTION COSH (n NUMBER) RETURN NUMBER;

If n is a real number and i = √-1 (the imaginary square root of -1), then the relationship between COS and COSH can be expressed as follows:

COS (i * n) = COSH (h)

13.1.9 The EXP function

The EXP function returns the value e raised to the n th power, where n is the input argument. The specification for the EXP function is:

FUNCTION EXP (n NUMBER) RETURN NUMBER;

The number e (approximately equal to 2.71828) is the base of the system of natural logarithms.

13.1.10 The FLOOR function

The FLOOR function, the opposite of the CEIL function, returns the largest integer that is less than or equal to the input number. The specification for the FLOOR function is:

FUNCTION FLOOR (n NUMBER) RETURN NUMBER;

Here are some examples of the values returned by FLOOR:

FLOOR (6.2) ==> 6
FLOOR (-89.4) ==> -90

For a comparison of FLOOR with several other numeric functions, see Section 13.1.23 later in this chapter.

13.1.11 The LN function

The LN function returns the natural logarithm of the input. The specification for the LN function is:

FUNCTION LN (n NUMBER) RETURN NUMBER;

The argument n must be greater than or equal to 0. If you pass LN a negative argument, you will receive the following error:

ORA-01428: argument '-1' is out of range

13.1.12 The LOG function

The LOG function returns the base -b logarithm of the input value. The specification for the LOG function is:

FUNCTION LOG (b NUMBER, n NUMBER) RETURN NUMBER;

The argument n must be greater than or equal to 0. The base b must be greater than 1. If you pass LOG an argument that violates either of these rules, you will receive the following error:

ORA-01428: argument '-1' is out of range

13.1.13 The MOD function

The MOD function returns the remainder of one number when divided by a second number. The specification for the MOD function is:

FUNCTION MOD (dividend NUMBER, divisor NUMBER) RETURN NUMBER;

If the divisor is zero, then the dividend is returned unchanged. Here are some examples of MOD:

MOD (10, 5) ==> 0
MOD (2, 1) ==> 0
MOD (3,2) == 1

You can use MOD to determine quickly if a number is odd or even:

FUNCTION is_odd (num_in IN NUMBER) RETURN BOOLEAN
IS
BEGIN
   RETURN MOD (num_in, 2) = 1;
END;

FUNCTION is_even (num_in IN NUMBER) RETURN BOOLEAN
IS
BEGIN
   RETURN MOD (num_in, 2) = 0;
END;

13.1.14 The POWER function

The POWER function raises the first argument to the power indicated by the second argument. The specification for the POWER function is:

FUNCTION POWER (base NUMBER, power NUMBER) RETURN NUMBER;

If base is negative, then power must be an integer. The following expression calculates the range of valid values for a BINARY_INTEGER variable (-2 ³¹ -1 through 2 ³¹ -1):

POWER (-2, 31) - 1 .. POWER (2, 31) - 1

or:

-2147483637 .. 2147483637 

13.1.15 The ROUND function

The ROUND function returns the first argument rounded to the number of decimal places specified in the second argument. The specification for the ROUND function is:

FUNCTION ROUND (n NUMBER, [decimal_places NUMBER]) RETURN NUMBER;

The decimal_places argument is optional and defaults to 0, which means that n will be rounded to zero decimal places, a whole number. The value of decimal_places can be less than zero. A negative value for this argument directs ROUND to round digits to the left of the decimal point, rather than to the right. Here are some examples:

ROUND (153.46) ==> 153
ROUND (153.46, 1) ==> 153.5
ROUND (153, -1) ==> 150

For a comparison of ROUND with several other numeric functions, see Section 13.1.23 later in this chapter.

13.1.16 The SIGN function

The SIGN function returns the sign of the input number. The specification for the SIGN function is:

FUNCTION SIGN (n NUMBER) RETURN NUMBER;

This function returns one of the three values shown below:

-1

n is less than zero

0

n is equal to zero

+1

n is greater than zero

13.1.17 The SIN function

The SIN trigonometric function returns the sine of the specified angle. The specification for the SIN function is:

FUNCTION SIN (angle NUMBER) RETURN NUMBER;

where angle must be expressed in radians. A radian is equal to 180/pi or roughly 57.29578. If your angle is specified in degrees, then you should call SIN as follows:

my_sine := SIN (angle_in_degrees/57.29578);

13.1.18 The SINH function

The SINH trigonometric function returns the hyperbolic sine of the specified number. The specification for the SINH function is:

FUNCTION SINH (n NUMBER) RETURN NUMBER;

If n is a real number and i = √-1 (the imaginary square root of -1), then the relationship between SIN and SINH can be expressed as follows:

SIN (i * n) = i * SINH (h)

13.1.19 The SQRT function

The SQRT function returns the square root of the input number. The specification for the SQRT function is:

FUNCTION SQRT (n NUMBER) RETURN NUMBER;

where n must be greater than or equal to 0. If n is negative, you will receive the following error:

ORA-01428: argument '-1' is out of range

13.1.20 The TAN function

The TAN trigonometric function returns the tangent of the specified angle. The specification for the TAN function is:

FUNCTION TAN (angle NUMBER) RETURN NUMBER;

where angle must be expressed in radians. A radian is equal to 180/pi or roughly 57.29578. If your angle is specified in degrees, then you should call TAN as follows:

my_tane := TAN (angle_in_degrees/57.29578);

13.1.21 The TANH function

The TANH trigonometric function returns the hyperbolic tangent of the specified number. The specification for the TANH function is:

FUNCTION TANH (n NUMBER) RETURN NUMBER;

If n is a real number and i = √-1 (the imaginary square root of -1), then the relationship between TAN and TANH can be expressed as follows:

TAN (i * n) = i * TANH (h)

13.1.22 The TRUNC function

The TRUNC function truncates the first argument to the number of decimal places specified by the second argument. The specification for the TRUNC function is:

FUNCTION TRUNC (n NUMBER, [decimal_places NUMBER]) RETURN NUMBER;

The decimal_places argument is optional and defaults to 0, which means that n will be truncated to zero decimal places, a whole number. The value of decimal_places can be less than zero. A negative value for this argument directs TRUNC to truncate or zero-out digits to the left of the decimal point, rather than to the right. Here are some examples:

TRUNC (153.46) ==> 153
TRUNC (153.46, 1) ==> 153.4
TRUNC (-2003.16, -1) ==> -2000

13.1.23 Rounding and Truncation with PL/SQL

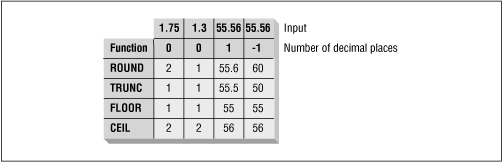
There are four different numeric functions that perform rounding and truncation actions: CEIL, FLOOR, ROUND, and TRUNC. It is easy to get confused about which of the functions to use in a particular situation. The following table compares functions. Figure 13.1 illustrates the use of the functions for different values and decimal place rounding.

Figure 13.1: Impact of rounding and truncating functions