Next: Шина (Bus) Up: Введение в сети Previous: Сети с выделенным сервером Contents Index

Сетевые топологии

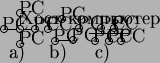
Термин ``топология'', или ``топология сети'', характеризует физическое расположение компьютеров, кабелей и других компонентов сети. Кроме термина ``топология'', иногда для описания физической компоновки употребляют также термины «физическое расположение», «компоновка», «диаграмма», «карта». Топология сети обуславливает ее характеристики. В частности, выбор той или иной топологии влияет на состав необходимого сетевого оборудования, на характеристики сетевого оборудования, на возможности расширения сети и способ управления сетью.

Чтобы совместно использовать ресурсы или выполнять другие сетевые задачи компьютеры должны быть подключены друг к другу. Для этой цели в большинстве сетей применяется кабель. Топология определяет способ взаимодействия компьютеров в сети. Различным видам топологий соответствуют различные методы взаимодействия, и эти методы оказывают большое влияние на сеть.

Базовые топологии

0.1mm
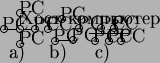
$\begin{picture}(1340,511) \put(198,311){\circle{80}} \put(198,351){\line(0,1){10... ...{\line(0,1){40}} \put(78,11){a)} \put(498,11){b)} \put(978,11){c)} \end{picture}$

Рис. 1. Сетевые топологии. a - звезда, b - кольцо, c - шина.

Существуют три основные сетевые топологии:

Звездообразная сеть, звезда (star).: В этом случае рабочие станции соединены напрямую с компьютером, выполняющим объединяющие функции в сети. Это может быть файл-сервер или хост-компьютер.
Кольцевая сеть, кольцо (ring).: Все компьютеры в сети увязаны друг с другом в кольце, при этом сообщение передающей станции прежде чем достигнет адресата может пройти через множество других.
Шинная сеть, шина (bus): Все компьютеры сети подключены к центральному кабелю (иногда называемому магистраль или шина).

Хотя сами по себе базовые топологии несложны, в реальности часто встречаются довольно сложные комбинации, объединяющие свойства нескольких топологий.

Помимо трех вышеперечисленных при небольшом числе узлов сети используюся несколько других топологий. В их числе встречаются полносвязная, куб, гиперкуб, гипертетраэдр. Данные топологии обеспечивают наиболее эффективный с точки зрения быстродействия обмен данными между узлами и чаще всего используются для реализации тесносвязанных конфигураций из для высокопроизводительных вычислительных комплексов и коммутационных устройств.

0.1mm
$\begin{picture}(1128,318) \put(148,248){\circle{60}} \put(148,28){\circle{60}} \... ...{40}} \put(658,248){\line(3,2){40}} \put(658,38){\line(3,2){36}} \end{picture}$

Рис. 2. Топологии: тетраэдр, куб, полносвязная.

Subsections

Alex Otwagin 2002-12-16