8.6.3. Discussion

This is a beautiful example of a solution that may not be obvious. We read every line in the file but don't have to store them all in memory. This is great for large files. Each line has a 1 in N (where N is the number of lines read so far) chance of being selected.

Here's a replacement for fortune using this algorithm:

$/ = "%%\n";
@ARGV = ("/usr/share/games/fortunes") unless @ARGV;
srand;
rand($.) < 1 && ($adage = $_) while <>;
print $adage;

If you know line offsets (for instance, you've created an index) and the number of lines, you can randomly select a line and jump to its offset in the file, but you usually don't have such an index.

Here's a more rigorous explanation of how the algorithm works. The function call rand ($.) picks a random number between 0 and the current line number. Therefore, you have a one in N chance, that is, 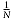, of keeping the Nth line. Therefore you've a 100% chance of keeping the first line, a 50% chance of keeping the second, a 33% chance of keeping the third, and so on. The question is whether this is fair for all N, where N is any positive integer.

First, some concrete examples, then abstract ones.

Obviously, a file with one line (N=1) is fair: you always keep the first line because 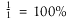= 100%, making it fair for files of 1 line. For a file with two lines, N=2. You always keep the first line; then when reaching the second line, you have a 50% chance of keeping it. Thus, both lines have an equal chance of being selected, which shows that N=2 is fair. For a file with three lines, N=3. You have a one-third chance, 33%, of keeping that third line. That leaves a two-thirds chance of retaining one of the first two out of the three lines. But we've already shown that for those first two lines there's a 50-50 chance of selecting either one. 50 percent of two-thirds is one-third. Thus, you have a one-third chance of selecting each of the three lines of the file.

In the general case, a file of N+1 lines will choose the last line 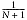times and one of the previous N lines 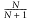times. Dividing 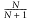by N leaves us with 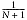for each the first N lines in our N+1 line file, and also 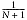for line number N+1. The algorithm is therefore fair for all N, where N is a positive integer.

We've managed to fairly choose a random line from a file with speed directly proportional to the size of the file, but using no more memory than it takes to hold the longest line, even in the worst case.