Используем средства библиотеки OpenSSL для криптографической защиты данных
Владимир Мешков
Самым надежным способом скрыть информацию от посторонних глаз является ее шифрование. В настоящее время существует большое количество стойких криптографических алгоритмов, позволяющих надежно защитить конфиденциальные данные и множество их программных реализаций, доступных для свободного использования.
Сегодня мы поговорим о библиотеке OpenSSL. Эта свободно распространяемая библиотека предоставляет в распоряжение пользователя набор утилит, реализующих различные криптографические алгоритмы, такие как Triple-DES, Blowfish, AES, RSA и другие.
Порядок использования утилит был подробно описан Всеволодом Стаховым в статье "Теория и практика OpenSSL" [1].
Кроме готовых к применению утилит, библиотека содержит набор функций, с помощью которых пользователь может разрабатывать собственные программы для криптографической защиты данных или создавать расширения, не входящие в стандартный набор. Большинство этих функций достаточно хорошо документированы, и наличие примеров программ значительно облегчает задачу изучения порядка их использования.
Не углубляясь в детали реализации алгоритмов, рассмотрим несколько практических примеров использования библиотеки OpenSSL для генерации псевдослучайных чисел, вычисления хэшей и шифрования данных с использованием симметричных и асимметричных алгоритмов. Основное внимание акцентируем на вопросах, которые, на мой взгляд, недостаточно полно освещены в официальной документации и требуют более детальной проработки.
Далее по тексту библиотека OpenSSL будет именоваться просто библиотека, кроме специально оговоренных случаев.
Генерация псевдослучайной последовательности
Сгенерировать псевдослучайную последовательность (ПСП) при помощи библиотеки очень просто. Для этого достаточно вызвать функцию RAND_bytes, передав ей в параметрах указатель на буфер для хранения сгенерированной последовательности и размер этого буфера. Следующий код демонстрирует это:
Листинг 1. Генерация ПСП
#include <openssl/rand.h>
void main()
{
int outf;
unsigned char buf[1024];
if(RAND_bytes(buf, sizeof(buf))) { /* 1 succes, 0 otherwise */
outf = open("./rnd_bytes", O_CREAT|O_TRUNC|O_RDWR, 0600);
write(outf, buf, sizeof(buf));
} else printf("-ERR: RAND_bytes\n");
}
Сохраним этот код в файле rand_test.c и получим исполняемый файл формата ELF при помощи команды:
gcc -o rand_test rand_test.c -lssl
После запуска на выполнение файла rand_test в текущем каталоге будет создан файл rnd_bytes размером 1024 байта, содержащий сгенерированную ПСП.
Вычисление хэшей
Хэш - это механизм контроля целостности данных, обладающий специальными свойствами:
n зная сообщение, легко вычислить хэш. Обратная задача нахождения сообщения по известному хэшу является вычислительно-трудоемкой;
n для заданного сообщения хэш является уникальным, т.е. не должно существовать двух разных сообщений с одинаковыми хэшами.
Из всех существующих алгоритмов хэширования наибольшее распространение получил алгоритм MD5. Аббревиатура "MD" означает Message Digest (краткое изложение сообщения, или дайджест). В соответствии с этим алгоритмом, входной текст обрабатывается 512-битовыми блоками, разбитыми на шестнадцать 32-битовых подблоков. Выходом алгоритма является набор из четырех 32-битовых блоков, которые объединяются в единое 128-битное значение. Рассмотрим, как вычисляется хэш сообщения по алгоритму MD5 с использованием средств библиотеки.
Для вычисления хэша библиотека предоставляет в наше распоряжение функцию MD5:
unsigned char * MD5(const unsigned char *d, unsigned long n, unsigned char *md)
Эта функция принимает три параметра - указатель на буфер с исходными данными d, размер этого буфера n и указатель на буфер для хранения вычисленного хэша md. Это очень простая в использовании функция, но у нее есть недостаток - она пригодна для вычисления хэша данных, которые можно полностью разместить в оперативной памяти. Для файлов большого размера вычисление хэша производится поэтапно. Для этого библиотека предоставляет следующий набор функций (см. openssl/md5.h):
void MD5_Init(MD5_CTX * ctx);
void MD5_Update(MD5_CTX * ctx, const void * data, unsigned long len);
void MD5_Final(unsigned char * md, MD5_CTX * ctx);
Функция MD5_Init() инициализирует контекст дайджеста - структуру, определенную в файле openssl/md5.h:
typedef struct MD5state_st {
MD5_LONG A,B,C,D;
MD5_LONG Nl,Nh;
MD5_LONG data[MD5_LBLOCK]; /* MD5_LBLOCK = 16 */
int num;
} MD5_CTX;
Инициализация контекста подразумевает его заполнение определенными значениями (см. файл md5_dgst.c исходных текстов библиотеки):
#define INIT_DATA_A (unsigned long)0x67452301L
#define INIT_DATA_B (unsigned long)0xefcdab89L
#define INIT_DATA_C (unsigned long)0x98badcfeL
#define INIT_DATA_D (unsigned long)0x10325476L
int MD5_Init(MD5_CTX *c)
{
c->A=INIT_DATA_A;
c->B=INIT_DATA_B;
c->C=INIT_DATA_C;
c->D=INIT_DATA_D;
c->Nl=0;
c->Nh=0;
c->num=0;
return 1;
}
Функция MD5_Update() вычисляет хэш. Входными параметрами этой функции являются указатель на контекст хэша ctx, указатель на блок входных данных data и размер этого блока len. Функция MD5_Final() помещает вычисленный хэш из контекста ctx в выходной буфер md, размер которого должен быть равен 16 байт.
Листинг 2 демонстрирует порядок использования перечисленных выше функций для вычисления хэша файла:
Листинг 2. Вычисление MD5-хэша для файла большого размера
#include <openssl/md5.h>
#define BUFSIZE (1025*16)
void main(int argc, char **argv)
{
MD5_CTX c; /* контекст хэша */
unsigned char buf[BUFSIZE];
unsigned char md_buf[MD5_DIGEST_LENGTH];
/* В командной строке передается имя файла, для которого вычисляется хэш */
int inf = open(argv[1], O_RDWR);
/* Инициализируем контекст */
MD5_Init(&c);
/* Вычисляем хэш */
for(;;) {
int i = read(inf, buf, BUFSIZE);
if(i <= 0) break;
MD5_Update(&c, buf, (unsigned long)i);
}
/* Помещаем вычисленный хэш в буфер md_buf */
MD5_Final(md_buf, &c);
/* Отображаем результат */
for(i = 0; i < MD5_DIGEST_LENGTH; i++) printf("%02x", md_buf[i]);
}
Проверить правильность вычисления хэша можно при помощи утилиты md5sum.
В рассмотренном листинге мы обращаемся к функциям библиотеки напрямую. В документации рекомендуется использовать высокоуровневые функции с префиксом EVP вместо прямого вызова функций алгоритма хэширования. Разберемся подробнее, что это за EVP-функции.
Библиотека поддерживает внутреннюю таблицу, в которой каждый элемент представляет собой структуру, содержащую адреса функций алгоритмов шифрования и хэширования, реализованных в библиотеке. Для работы с высокоуровневыми функциями необходимо извлечь структуру требуемого алгоритма из этой таблицы, получив, таким образом, адреса его функций. Но прежде эту таблицу необходимо заполнить. Адреса функций алгоритмов хэширования записываются в таблицу при помощи функции OpenSSL_add_all_digests(), адреса функций алгоритмов шифрования - при помощи функции OpenSSL_add_all_ciphers().
Извлечь структуру требуемого алгоритма хэширования из таблицы можно при помощи функции EVP_get_digestbyname(const char * name), где name является символьным обозначением алгоритма. Для алгоритма MD5 это будет "md5". Список всех имен приведен в файле openssl/object.h. Результат работы функции EVP_get_digestbyname() сохраняется в структуре типа EVP_MD:
struct env_md_st
{
int type;
int pkey_type;
int md_size;
unsigned long flags;
int (*init)(EVP_MD_CTX *ctx);
int (*update)(EVP_MD_CTX *ctx,const void *data,unsigned long count);
int (*final)(EVP_MD_CTX *ctx,unsigned char *md);
int (*copy)(EVP_MD_CTX *to,const EVP_MD_CTX *from);
int (*cleanup)(EVP_MD_CTX *ctx);
/* FIXME: prototype these some day */
int (*sign)();
int (*verify)();
int required_pkey_type[5]; /*EVP_PKEY_xxx */
int block_size;
int ctx_size; /* how big does the ctx->md_data need to be */
} /* EVP_MD */;
Эта структура определена в файле openssl/evp.h. В ее состав входят указатели на функции алгоритма хэширования. При вызове функции EVP_get_digestbyname() в эти указатели будут записаны реальные адреса функций библиотеки для работы с выбранным типом алгоритма хэширования, и в дальнейшем все вызовы функций будут выполняться косвенно через эти указатели. Получив адреса библиотечных функций, необходимо заполнить контекст для вычисления хэша - структуру типа EVP_MD_CTX (см. openssl/evp.h):
struct env_md_ctx_st
{
const EVP_MD *digest;
ENGINE *engine;
unsigned long flags;
void *md_data;
} /* EVP_MD_CTX */;
Заполнение контекста выполняется при помощи функции EVP_DigestInit(). В параметрах этой функции передаются указатели на контекст для вычисления хэша и на структуру, содержащую адреса функций алгоритма хэширования:
EVP_DigestInit(EVP_MD_CTX * ctx, EVP_MD * md)
Функция копирует структуру "EVP_MD * md" в контекст дайджеста путем приравнивания соответствующих указателей (см. файл crypto/evp/digest.c исходных текстов библиотеки):
ctx->digest = md;
Заполнив контекст, мы получаем возможность вызывать библиотечные функции для вычисления хэша, используя адреса, которые сохранены в структуре digest-контекста. Вычисление хэша выполняет функция EVP_DigestUpdate(), функция EVP_DigestFinal() копирует вычисленный хэш из контекста дайджеста в выходной буфер:
int EVP_DigestUpdate(EVP_MD_CTX *ctx, const void *d, unsigned int cnt);
int EVP_DigestFinal(EVP_MD_CTX *ctx, unsigned char *md, unsigned int *s);
Параметры функции EVP_DigestUpdate - указатель на контекст для вычисления хэша ctx, буфер d для хранения промежуточного результата вычисления и размер этого буфера cnt. Функция EVP_DigestFinal сохраняет размер вычисленного хэша в последнем параметре *s.
По завершении работы контекст для вычисления хэша очищается при помощи функции EVP_MD_CTX_cleanup().
Листинг 3 демонстрирует порядок использования высокоуровневых функций библиотеки для вычисления хэша файла по алгоритму MD5.
Листинг 3. Вычисление MD5-хэша файла с использованием высокоуровневых функций библиотеки
#include <openssl/md5.h>
#include <openssl/evp.h>
#define BUFSIZE (1025*16)
void main(int argc, char **argv)
{
EVP_MD_CTX mdctx; /* контекст для вычисления хэша */
const EVP_MD * md; /* структура с адресами функций алгоритма */
unsigned char md_value[EVP_MAX_MD_SIZE];
int md_len; /* размер вычисленного хэша */
/* В командной строке передаем имя файла, для которого вычисляется хэш */
int inf = open(argv[1], O_RDWR);
/* Добавляем алгоритмы хэширования во внутреннюю таблицу библиотеки */
OpenSSL_add_all_digests();
/* Получаем адреса функций алгоритма MD5 и инициализируем контекст для вычисления хэша */
md = EVP_get_digestbyname("md5");
EVP_DigestInit(&mdctx, md);
/* Вычисляем хэш */
for(;;) {
i = read(inf, buf, BUFSIZE);
if(i <= 0) break;
EVP_DigestUpdate(&mdctx, buf, (unsigned long)i);
}
/* Копируем вычисленный хэш в выходной буфер. Размер хэша сохраняем в переменной md_len */
EVP_DigestFinal(&mdctx, md_value, &md_len);
/* Очищаем контекст */
EVP_MD_CTX_cleanup(&mdctx);
/* Отобразим результат */
for(i = 0; i < md_len; i++) printf("%02x", md_value[i]);
}
Универсальность метода использования функций высокого уровня очевидна - для расчета хэша по новому алгоритму достаточно изменить только его название в функции EVP_get_digestbyname. Поэтому именно этот метод рекомендуется к использованию разработчиками библиотеки.
Симметричные алгоритмы шифрования
Целью шифрования информации является предотвращение угрозы нарушения ее конфиденциальности, т.е. несанкционированное ознакомление с ней. Алгоритмы шифрования можно разделить на две основные категории:
n симметричное шифрование;
n ассиметричное шифрование.
В алгоритмах симметричного шифрования используется один и тот же ключ для шифрования и расшифровки сообщения. Это означает, что любой, кто имеет доступ к ключу шифрования, может расшифровать сообщение. Алгоритмы симметричного шифрования именно поэтому и называют алгоритмами с секретным ключом - ключ шифрования должен быть доступен только тем, кому предназначено сообщение. Симметричное шифрование идеально подходит для шифрования информации "для себя", например, с целью отсечь несанкционированный доступ к ней в отсутствии владельца.
Библиотека поддерживает большое количество симметричных алгоритмов. Некоторые из них мы сейчас рассмотрим, и начнем с самого знаменитого - с DES.
Алгоритм DES
Алгоритм DES (Data Encryption Standart, стандарт шифрования данных) был разработан в 1973 году компанией IBM и долгое время являлся основным стандартом шифрования в мире. Этот алгоритм использует 56-битный ключ и шифрует данные блоками по 64 бита. Имеет несколько режимов работы, которые применимы и для других блочных шифров симметричной схемы:
n Режим электронной шифровальной книги Electronic Codebook Mode (ECB). Простейший режим. Открытый текст обрабатывается блоками по 64 бита (8 байт) и каждый блок шифруется с одним и тем же ключом (см. рис. 1). Самой важной особенностью режима ECB является то, что одинаковые блоки открытого текста в шифрованном тексте будут также представляться одинаковыми блоками. Поэтому при передаче достаточно длинных сообщений режим ECB не может обеспечить необходимый уровень защиты. Если сообщение имеет явно выраженную структуру, у криптоаналитика появляется возможность использовать регулярности текста. Например, если известно, что в начале сообщения всегда размещается определенный заголовок, криптоаналитик может получить в свое распоряжение целый набор соответствующих пар блоков открытого и шифрованного текста.
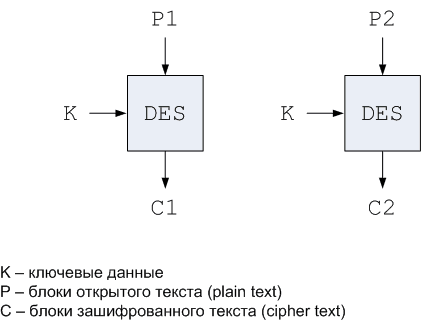
Рисунок 1. Режим электронной шифровальной книги ECB
n Режим сцепления шифрованных блоков Cipher Block Chaining Mode (CBC). Эта технология свободна от недостатков режима ECB. В режиме CBC входной блок данных для алгоритма шифрования вычисляется как результат операции XOR текущего блока открытого текста и блока шифрованного текста, полученного на предыдущем шаге (см. рис. 2).
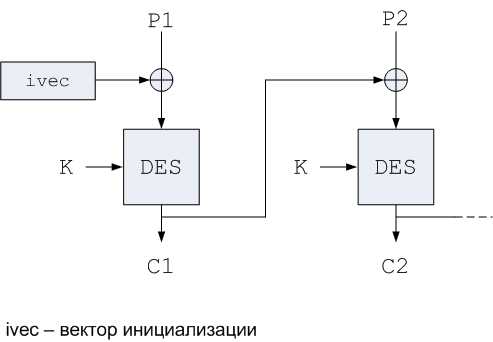
Рисунок 2. Режим сцепления шифрованных блоков CBC
n Режим шифрованной обратной связи Cipher Feedback Mode (CFB). Полученный на предыдущем шаге шифрованный текст используется как входные данные для алгоритма шифрования с целью получения псевдослучайной последовательности (ПСП), XOR-разница которой и блока открытого текста определяет очередной блок шифрованного текста (см. рис. 3)
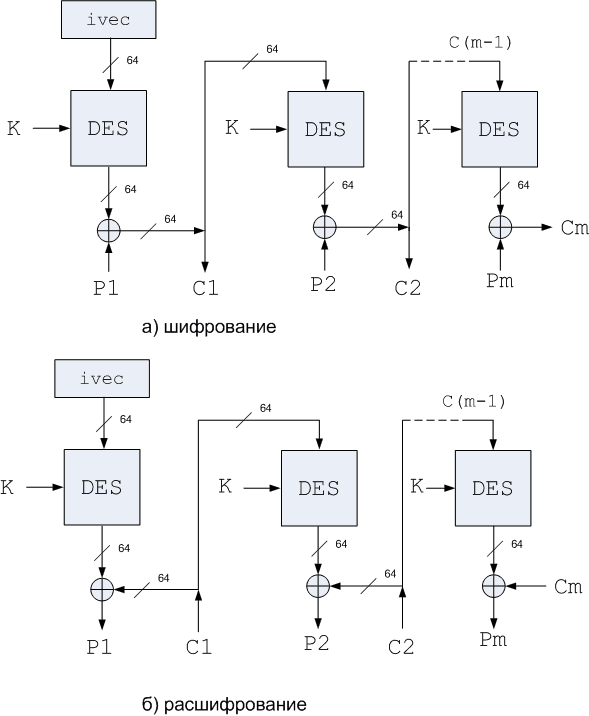
Рисунок 3. Режим 64-битовой шифрованной обратной связи CFB
n Режим обратной связи по выходу Output Feedback Mode (OFB). Работает подобно CFB, но в качестве входных данных для алгоритма шифрования используются ранее полученные выходные данные DES (см. рис. 4).
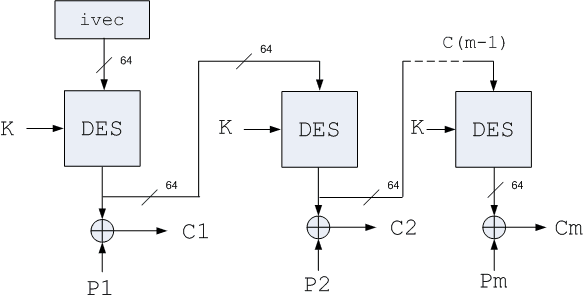
Рисунок 4. Режим 64-битовой обратной связи по выходу OFB
Если проводить аналогии с алгоритмом ГОСТ 2814789, то режим ECB соответствует режиму простой замены, OFB - режиму гаммирования, CFB - режиму гаммирования с обратной связью.
Малая длина ключа и постоянно растущая мощность современных вычислительных комплексов сделали алгоритм DES потенциально уязвимым перед атакой, основанной на полном переборе ключей. Это обстоятельство наложило существенные ограничения на использование DES в чистом виде и потребовало поиска альтернативы данному шифру. Один из вариантов решения проблемы предполагал создание совершенно нового алгоритма, другой подход сделал ставку на многократное шифрование с помощью DES с применением нескольких ключей.
Широкое распространение получил "тройной" DES (Triple-DES), представляющий собой последовательность операций шифрования-дешифрования-шифрования (EDE - encrypt-decrypt-encrypt) с использованием трех разных ключей. Схема "тройного" DES представлена на рис. 5.
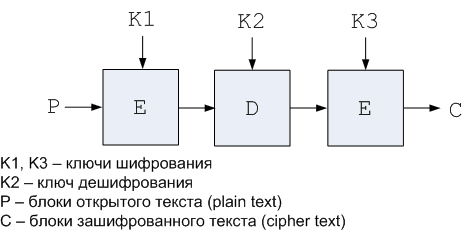
Рисунок 5. Схема "тройного" DES
"Тройной" DES может также использовать два ключа. В этом случае операции шифрования выполняются на одном ключе, а операция дешифрования - на другом.
Использование функций библиотеки, реализующих алгоритм DES, предполагает два этапа: генерация ключей и собственно шифрование информации.
Генерацию DES-ключа выполняет функция DES_random_key(DES_cblock *ret). Входным параметром функции является указатель на блок данных типа DES_cblock, в котором будет сохранен ключ. Тип DES_cblock определен в файле openssl/des.h, и представляет собой 8-байтовую последовательность с контролем четности. Младший значащий бит каждого байта является битом четности:
typedef unsigned char DES_cblock[8];
После генерации ключ необходимо сконвертировать в платформенно-зависимый формат при помощи функции DES_set_key_checked(const_DES_cblock *key, DES_key_schedule *schedule). Функция принимает два параметра - указатель на сгенерированный ключ и указатель на структуру типа DES_key_schedule. Этот структурный тип определен в файле openssl/des.h. Функция DES_set_key_checked выполняет контроль четности всех байт ключа и проверяет, можно ли использовать его для шифрования, т.е. является ключ криптографически сильным или нет. Если четность байт не соблюдается, функция возвращает -1. Если сгенерированный ключ оказался криптографически слабым (weak), функция возвращает -2. Если ключ удовлетворяет всем требованиям, то он конвертируется в платформенно-зависимый формат и помещается в структуру schedule.
Исходя из вышеизложенного, код генератора ключевой последовательности для алгоритма Triple-DES будет выглядеть следующим образом:
Листинг 4. Генератор ключей для алгоритма Triple-DES
#include <openssl/des.h>
int main()
{
int key, i = 0, j = 0;
DES_cblock cb;
DES_key_schedule ks;
/* Создаем ключевой файл */
key = open(KEYS, O_CREAT|O_TRUNC|O_RDWR, 0600);
/* Генерируем три ключа */
for(; i < 3; i++) {
DES_random_key(&cb);
if((j = DES_set_key_checked(&cb, &ks)) != 0) return j;
if(write(key, (unsigned char *)&ks, DES_SCHEDULE_SZ) < 0) return -1;
}
}
Операцию криптопреобразования по алгоритму Triple-DES с тремя ключами и 64-битной обратной связью по выходу (режим OFB) выполняет функция DES_ede3_ofb64_encrypt:
void DES_ede3_ofb64_encrypt(const unsigned char *in, unsigned char *out, long length, DES_key_schedule *ks1, \
DES_key_schedule *ks2, DES_key_schedule *ks3, DES_cblock *ivec, int *num);
В параметрах функции передаются:
n указатели на блоки незашифрованных и зашифрованных данных in и out;
n размер данных для шифрования length;
n ключи шифрования ks1, ks2, ks3;
n указатель на вектор инициализации ivec (начальное заполнение блока ivec, см. рис. 2-4);
Разъясним назначение последнего параметра int *num. Шифрование выполняется блоками по 64 бита, но длина входного сообщения (файла) не обязательно должна быть кратна этому значению. Например, файл размером 26 байт состоит из трех целых 8-байтовых блоков, а из четвертого блока используются только 2 байта. Так вот значение num показывает, сколько байт последнего 8-байтового блока мы используем, или, как сказано в документации, "how much of the 64bit block we have used is contained in *num" (см. комментарии к функции DES_ede3_ofb64_encrypt, файл crypto/des/ofb64ede.c исходных текстов библиотеки).
Листинг 5. Фрагмент программы для криптопреобразования файла по алгоритму Triple-DES с использованием трех ключей и 64-битной обратной связи по выходу
/* Буферы для входных и выходных (зашифрованных) данных */
unsigned char inbuf[1024], outbuf[1024];
/* Структура для хранения ключевых данных */
DES_key_schedule ks1, ks2, ks3;
/* Считываем три ранее созданных ключа
(key - дескриптор ключевого файла) */
read(key,(unsigned char *)&ks1, DES_SCHEDULE_SZ);
read(key,(unsigned char *)&ks2, DES_SCHEDULE_SZ);
read(key,(unsigned char *)&ks3, DES_SCHEDULE_SZ);
/* Открываем входной и создаем выходной файлы */
. . . .
/* Шифруем файл */
for(;;) {
inlen = fread(inbuf, 1, 1024, in);
if(inlen <= 0) break;
DES_ede3_ofb64_encrypt(inbuf, outbuf, (long)inlen, &ks1, &ks2, &ks3, (DES_cblock *)ivec, &num);
fwrite(outbuf, 1, inlen, out);
}
С перечнем всех функций, реализующих различные режимы алгоритма DES, можно ознакомиться на страницах руководства man des, описание режимов приведено в man des_modes.
Алгоритм Blowfish
Blowfish - симметричный блочный шифр, разработанный Брюсом Шнайером (Bruce Schneier). Этот шифр использует ключи разной длины, обычно 128 бит, и шифрует данные блоками по 64 бита. Алгоритм поддерживает такие же режимы, как и DES (см. раздел "Алгоритм DES"), и считается одним из самых быстрых в своем классе.
Как и в случае алгоритма DES, использование Blowfish включает две стадии: генерацию ключевых данных и собственно криптопреобразование информации.
Генерация ключевых данных предполагает получение Nбитной случайной последовательности и последующее ее преобразование при помощи функции BF_set_key(), прототип которой определен в файле openssl/blowfish.h:
void BF_set_key(BF_KEY *key, int len, const unsigned char *data);
Задача этой функции - поместить ключ длиной len из буфера data в структуру key.
Криптопреобразование данных в режиме CFB c 64битной обратной связью выполняет функция BF_cfb64_encrypt:
void BF_cfb64_encrypt(const unsigned char *in, unsigned char *out, long length, const BF_KEY *schedule, unsigned char *ivec, int *num, int enc);
Думаю, что после того как мы рассмотрели DES, никому не составит труда разобраться в назначении параметров этой функции. Остановимся только на последнем параметре - int enc. Он задает режим работы алгоритма и может принимать два значения: BF_ENCRYPT для режима шифрования и BF_DECRYPT для режима дешифрования. Оба эти значение определены в файле openssl/blowfish.h:
#define BF_ENCRYPT 1
#define BF_DECRYPT 0
А теперь оформим все теоретические выкладки в виде функции криптографического преобразования информации по алгоритму Blowfish, работающему в режиме 64битной обратной связи (CFB-64).
Листинг 6. Функция криптографического преобразования информации по алгоритму Blowfish, режим 64-битной обратной связи (CFB-64)
#include <openssl/blowfish.h>
#define BUFSIZE 1024
/* Функция криптопреобразования информации. Параметры функции: дескрипторы входного и выходного
файлов и режим работы - BF_ENCRYPT для шифрования и BF_DECRYPT для дешифрования */
int do_crypt(FILE *in, FILE *out, int mode)
{
int num = 0;
unsigned char inbuf[BUFSIZE], outbuf[BUFSIZE];
/* Ключ шифрования длиной 128 бит и вектор инициализации */
const unsigned char key[16];
unsigned char iv[8];
BF_KEY bfkey;
/* Помещаем ключ в структуру bfkey */
BF_set_key(&bfkey, sizeof(key), key);
/* Шифруем блоки входного файла */
for(;;) {
int inlen = fread(inbuf, 1, BUFSIZE, in);
if(inlen <= 0) break;
BF_cfb64_encrypt(inbuf, outbuf, (long)inlen, &bfkey, iv, &num, mode);
fwrite(outbuf, 1, inlen, out);
}
return 1;
}
Следующий фрагмент функции иллюстрирует порядок криптопреобразования по алгоритму Blowfish, режим 64битной обратной связи по выходу (OFB-64).
Листинг 7. фрагмент функции криптографического преобразования информации по алгоритму Blowfish, режим 64-битной обратной связи по выходу (OFB-64)
void do_crypt(FILE *in, FILE *out)
{
unsigned char inbuf[BUFSIZE];
unsigned char outbuf[BUFSIZE];
/* Ключ и вектор инициализации */
. . .
BF_set_key(&bfkey, KEY_SIZE, key);
for(;;) {
int inlen = fread(inbuf, 1, BUFSIZE, in);
if(inlen <= 0) break;
BF_ofb64_encrypt(inbuf, outbuf, (long)inlen, &bfkey, iv, &num);
fwrite(outbuf, 1, inlen, out);
}
}
Использование высокоуровневых функций библиотеки для шифрования
Как и в случае алгоритмов хэширования (см. раздел "Вычисление хэшей"), разработчики библиотеки рекомендуют использовать функции высокого уровня вместо прямого обращения к функциям алгоритма шифрования. Порядок использования высокоуровневых функций шифрования и хэширования идентичен - в обоих случаях необходимо создать и инициализировать контекст, записав в него адреса функций необходимых алгоритмов. Адреса выбираются из внутренней таблицы, куда они попадают при помощи функции OpenSSL_add_all_ciphers().
Контекст алгоритма шифрования представляет собой структуру типа EVP_CIPHER_CTX, определенную в файле openssl/evp.h. Первым элементом этой структуры является указатель на структурный тип EVP_CIPHER следующего вида:
struct evp_cipher_st {
int nid;
int block_size;
int key_len; /* Default value for variable length ciphers */
int iv_len;
unsigned long flags; /* Various flags */
int (*init)(EVP_CIPHER_CTX *ctx, const unsigned char *key, const unsigned char *iv, int enc); /* init key */
int (*do_cipher)(EVP_CIPHER_CTX *ctx, unsigned char *out, const unsigned char *in, unsigned int inl);/* encrypt/decrypt data */
int (*cleanup)(EVP_CIPHER_CTX *); /* cleanup ctx */
int ctx_size; /* how big ctx->cipher_data needs to be */
int (*set_asn1_parameters)(EVP_CIPHER_CTX *, ASN1_TYPE *);
int (*get_asn1_parameters)(EVP_CIPHER_CTX *, ASN1_TYPE *);
int (*ctrl)(EVP_CIPHER_CTX *, int type, int arg, void *ptr);
void *app_data; /* Application data */
} /* EVP_CIPHER */;
Этот структурный тип содержит в своем составе указатели на функции, которые заполняются необходимыми нам значениями - адресами функций соответствующих алгоритмов. Получить адреса этих функций можно двумя способами.
Первый способ подразумевает поиск по символьному имени алгоритма:
OpenSSL_add_all_ciphers();
const EVP_CIPHER * cipher = EVP_get_cipherbyname("des_cbc");
Функция EVP_get_cipherbyname(const char * name) извлекает адреса функций алгоритма шифрования из внутренней таблицы библиотеки и заполняет структуру cipher. Входные параметры функции - символьное имя алгоритма, в данном случае это DES, режим CBC. Перечень всех имен содержится в файле openssl/object.h.
Второй способ - прямое обращение к нужной EVP-функции:
const EVP_CIPHER *cipher = EVP_des_cbc();
Получив адреса функций, инициализируем контекст алгоритма:
EVP_CIPHER_CTX_init(EVP_CIPHER_CTX *ctx);
EVP_EncryptInit(EVP_CIPHER_CTX *ctx, const EVP_CIPHER *cipher, const unsigned char *key, const unsigned char *iv);
Функция EVP_CIPHER_CTX_init обнуляет структуру, выделенную под контекст. Инициализацию контекста выполняет функция EVP_EncryptInit(). Параметры функции - указатель на контекст алгоритма ctx, структура с адресами библиотечных функций алгоритма cipher, блок с ключевыми данными key и вектор инициализации iv.
После инициализации контекста можно приступать к операции шифрования. Делает это функция EVP_EncryptUpdate():
int EVP_EncryptUpdate(EVP_CIPHER_CTX *ctx, unsigned char *out, int *outl, const unsigned char *in, int inl);
Функция шифрует inl байтов из буфера in и записывает зашифрованные данные в буфер out. В переменной outl сохраняется количество зашифрованных байтов.
Если размер сообщения не кратен размеру блока шифрования, то выполняется вызов функции EVP_EncryptFinal, которая "дошифровывает" оставшиеся данные:
int EVP_EncryptFinal(EVP_CIPHER_CTX *ctx, unsigned char *out, int *outl);
Следующий код демонстрирует использование функций высокого уровня для шифрования файла по алгоритму AES с ключом длиной 256 бит, режим 64-битовой шифрованной обратной связи CFB.
Листинг 8. Шифрование файла по алгоритму AES, длина ключа 256 бит, режим 64-битовой шифрованной обратной связи
#include <openssl/evp.h>
#define BUFSIZE 1024
int do_crypt(char *infile)
{
int outlen, inlen;
FILE *in, *out;
unsigned char key[32]; /* 256- битный ключ */
unsigned char iv[8]; /* вектор инициализации */
unsigned char inbuf[BUFSIZE], outbuf[BUFSIZE];
EVP_CIPHER_CTX ctx;
const EVP_CIPHER * cipher;
/* Обнуляем структуру контекста */
EVP_CIPHER_CTX_init(&ctx);
/* Выбираем алгоритм шифрования */
cipher = EVP_aes_256_cfb();
/* Инициализируем контекст алгоритма */
EVP_EncryptInit(&ctx, cipher, key, iv);
/* Шифруем данные */
for(;;) {
inlen = fread(inbuf, 1, BUFSIZE, in);
if(inlen <= 0) break;
if(!EVP_EncryptUpdate(&ctx, outbuf, &outlen, inbuf, inlen)) return 0;
fwrite(outbuf, 1, outlen, out);
}
if(!EVP_EncryptFinal(&ctx, outbuf, &outlen)) return 0;
fwrite(outbuf, 1, outlen, out);
EVP_CIPHER_CTX_cleanup(&ctx);
return 1;
}
Если мы захотим использовать другой алгоритм, нам достаточно будет заменить одну строку в исходном тексте. Например, для использования алгоритма Blowfish в режиме шифрованной обратной связи по выходу (OFB) необходимо заменить строку:
cipher = EVP_aes_256_cfb();
строкой:
cipher = EVP_bf_ofb();
а также задать правильную длину ключевых данных.
Список всех EVP-функций находится в файле openssl/evp.h.
Обратный процесс дешифрования информации отличается только названиями функций: вместо "EVP_EnryptInit" пишем "EVP_DecryptInit", вместо "EVP_EncryptUpdate" - "EVP_DecryptUpdate" и т. д. Фрагмент функции дешифрования файла, зашифрованного по алгоритму AES с 256-битным ключом в режиме 64-битовой обратной связи, представлен в листинге 9.
Листинг 9. Дешифрование файла, зашифрованного по алгоритму AES, длина ключа 256 бит, режим 64-битовой шифрованной ОС
int do_decrypt(char *infile)
{
/* Объявляем переменные */
. . . .
/* Обнуляем контекст и выбираем алгоритм дешифрования */
EVP_CIPHER_CTX_init(&ctx);
EVP_DecryptInit(&ctx, EVP_aes_256_cfb(), key, iv);
/* Открываем входной и создаем выходной файлы */
. . . .
/* Дешифруем данные */
for(;;) {
inlen = fread(inbuf, 1, BUFSIZE, in);
if(inlen <= 0) break;
if(!EVP_DecryptUpdate(&ctx, outbuf, &outlen,
inbuf, inlen)) return 0;
fwrite(outbuf, 1, outlen, out);
}
/* Завершаем процесс дешифрования */
if(!EVP_DecryptFinal(&ctx, outbuf, &outlen)) return 0;
. . . .
}
Работоспособность всех программ была проверена для ОС Linux Slackware 10.2, компилятор gcc-3.3.6, библиотека OpenSSL 0.9.7c. Исходные тексты всех программ, рассмотренных в данной статье, вы можете скачать с сайта http://bob.netport.com.ua/ssl.tar.gz.
Во второй части статьи мы рассмотрим примеры использования функций библиотеки для криптографической защиты данных с помощью ассиметричных алгоритмов.
Литература:
1. Стахов В. Теория и практика OpenSSL. - Журнал "Системный администратор", N1(2), январь 2003 г. - 17-26 с.
2. Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. - М.: Издательство ТРИУМФ, 2003 - 816 с.; ил.