Алгоритм Фокса

Next: Коммуникаторы Up: Коммуникаторы и топологии Previous: Коммуникаторы и топологии Contents

Алгоритм Фокса

Пусть перемножаемые матрицы $A=(a_{ij})$ и $B=(b_{ij})$ имеют порядок . Количество процессов является квадратом, квадратный корень которого кратен . В этом случае $p=q^{2}$ и $\bar{n}=n/q$ . В алгоритме Фокса матрицы разделяются среди процессов в виде клеток шахматной доски. При этом процессы рассматриваются как виртуальная двухмерная $q\times q$ сетка, и каждому процессу назначена подматрица $\bar{n}\times \bar{n}$ каждого множителя. Реализуется отображение:

$\begin{displaymath} \phi :\left\{ {0,1,...,p-1}\right\} \rightarrow \left\{ {(s,t):}0\leq s,t\leq q-1\right\} \end{displaymath}$

Оно определяет сетку процессов: процесс относится к строке и столбцу, заданному $\phi (i)$ . Процесс с рангом $\phi ^{-1}(s;t)$ назначается на подматрицы:

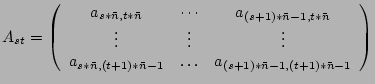
$A_{st}=\left(\begin{array}{ccc} a_{s*\bar{n},t*\bar{n}} & \cdots & a_{(s+1)*\b... ...+1)*\bar{n}-1} & \ldots & a_{(s+1)*\bar{n}-1,(t+1)*\bar{n}-1}\end{array}\right)$

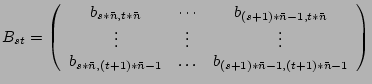
$B_{st}=\left(\begin{array}{ccc} b_{s*\bar{n},t*\bar{n}} & \cdots & b_{(s+1)*\b... ...+1)*\bar{n}-1} & \ldots & b_{(s+1)*\bar{n}-1,(t+1)*\bar{n}-1}\end{array}\right)$

Например, если , $\phi (x)=(x=3;xmod3)$ , и , то A будет разделена следующим образом (рис. 4).

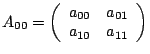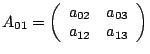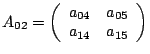Процесс 0: $A_{00}=\left(\begin{array}{cc} a_{00} & a_{01}\\ a_{10} & a_{11}\end{array}\right)$	Процесс 1: $A_{01}=\left(\begin{array}{cc} a_{02} & a_{03}\\ a_{12} & a_{13}\end{array}\right)$	Процесс 2: $A_{02}=\left(\begin{array}{cc} a_{04} & a_{05}\\ a_{14} & a_{15}\end{array}\right)$
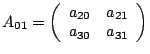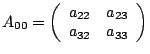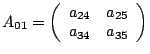Процесс 3: $A_{01}=\left(\begin{array}{cc} a_{20} & a_{21}\\ a_{30} & a_{31}\end{array}\right)$	Процесс 4: $A_{00}=\left(\begin{array}{cc} a_{22} & a_{23}\\ a_{32} & a_{33}\end{array}\right)$	Процесс 5: $A_{01}=\left(\begin{array}{cc} a_{24} & a_{25}\\ a_{34} & a_{35}\end{array}\right)$
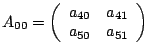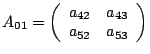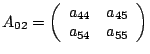Процесс 6: $A_{00}=\left(\begin{array}{cc} a_{40} & a_{41}\\ a_{50} & a_{51}\end{array}\right)$	Процесс 7: $A_{01}=\left(\begin{array}{cc} a_{42} & a_{43}\\ a_{52} & a_{53}\end{array}\right)$	Процесс 8: $A_{02}=\left(\begin{array}{cc} a_{44} & a_{45}\\ a_{54} & a_{55}\end{array}\right)$

Рис. 4. Разделение матрицы на подматрицы

В алгоритме Фокса, подматрицы блоков, $A_{rs}$ и $B_{st}$ , где , перемножаются и собираются в процессе $\phi ^{-1}(r;t)$ . Алгоритм состоит в следующем: