|
|
||||||
|
2.7 Обнаружение ошибок
Семенов Ю.А. (ГНЦ ИТЭФ) |
||||||
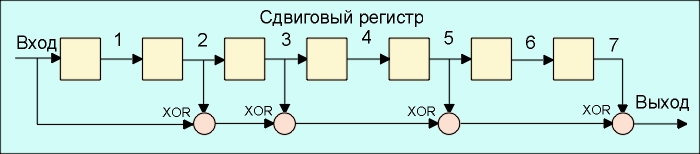
 Каналы передачи данных ненадежны, да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных (М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность). При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой - минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга. Пусть А и Б две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2. Можно показать, что для детектирования ошибок в n битах, схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N+1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N+1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями больше, чем оно может возникнуть из-за ошибок. Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится. Предположим, что частота ошибок (BER) равна р=10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1-(1-p)8=7,9х10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 бит равна 9p(1-p)8. Вероятность же реализации необнаруженной ошибки составит 1-(1-p)9 - 9p(1-p)8 = 3,6x10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать но и исправлять ошибки в одном из битов переданного блока. Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен и тогда предпочтительнее метод вычисления циклических сумм (CRC). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой. В Ethernet Вычисление crc производится аппаратно (см. также ethernet). На рис. 2.7.1. показан пример реализации аппаратного расчета CRC для образующего полинома B(x)= 1 + x2 + x3 +x5 + x7. В этой схеме входной код приходит слева. Рис. 2.7.1. Схема реализации расчета CRC Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r - степень образующего полинома.
|
||||||
|
Previous:
2.6.5 Статический алгоритм Хафмана
UP:
2.6 Методы сжатия информации
|