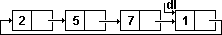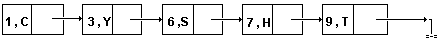Линейный список - это конечная последовательность однотипных элементов
(узлов), возможно, с повторениями. Количество элементов в последовательности
называется длиной списка, причем длина в процессе работы программы может
изменяться.
Линейный список F, состоящий из элементов D1,D2,...,Dn, записывают в виде
последовательности значений заключенной в угловые скобки F=, или
представляют графически (см.рис.12).
D1
| а
| D2
| а
| D3
| а
| ...
| а
| Dn
|
|---|
| Рис.12. Изображение линейного списка. |
Например, F1=< 2,3,1>,F2=< 7,7,7,2,1,12 >, F3=< >. Длина списков F1, F2, F3
равна соответственно 3,6,0.
При работе со списками на практике чаще всего приходится выполнять следующие
операции:
- найти элемент с заданным свойством;
- определить первый элемент в линейном списке;
- вставить дополнительный элемент до или после указанного узла;
- исключить определенный элемент из списка;
- упорядочить узлы линейного списка в определенном порядке.
В реальных языках программирования нет какой-либо структуры данных для
представления линейного списка так, чтобы все указанные операции над ним
выполнялись в одинаковой степени эффективно. Поэтому при работе с линейными
списками важным является представление используемых в программе линейных
списков таким образом, чтобы была обеспечена максимальная эффективность и по
времени выполнения программы, и по объему требуемой памяти.
Методы хранения линейных списков разделяются на методы последовательного и
связанного хранения. Рассмотрим простейшие варианты этих методов для списка с
целыми значениями F=<7,10>.
При последовательном хранении элементы линейного списка размещаются в
массиве d фиксированных размеров, например, 100, и длина списка указывается в
переменной l, т.е. в программе необходимо иметь объявления вида
float d[100]; int l;
Размер массива 100 ограничивает максимальные размеры линейного списка.
Список F в массиве d формируется так:
d[0]=7; d[1]=10; l=2;
Полученный список хранится в памяти согласно схеме на рис.13.
l: | 2 |
d: | 7
| 10
|
|
| ...
|
| |
|
| [0]
| [1]
| [2]
| [3]
|
| [98]
| [99] |
| Рис.13. Последовательное хранение линейного списка. |
|---|
При связанном хранении в качестве элементов хранения используются структуры,
связанные по одной из компонент в цепочку, на начало которой (первую структуру)
указывает указатель dl. Структура образующая элемент хранения, должна кроме
соответствующего элемента списка содержать и указатель на соседний элемент
хранения.
Описание структуры и указателя в этом случае может имееть вид:
typedef struct snd /* структура элемента хранения */
{ float val; /* элемент списка */
struct snd *n ; /* указатель на элемент хранения */
} DL;
DL *p; /* указатель текущего элемента */
DL *dl; /* указатель на начало списка */
Для выделения памяти под элементы хранения необходимо пользоваться функцией
malloc(sizeof(DL)) или calloc(l,sizeof(DL)). Формирование списка в связанном
хранении может осуществляется операторами:
p=malloc(sizeof(DL));
p->val=10; p->n=NULL;
dl=malloc(sizeof(DL));
dl->val=7; dl->n=p;
В последнем элементе хранения (конец списка) указатель на соседний элемент
имеет значение NULL. Получаемый список изображен на рис.14.
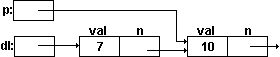
Рис.14. Связное хранение линейного списка.
При выборе метода хранения линейного списка следует учитывать, какие операции
будут выполняться и с какой частотой, время их выполнения и объем памяти,
требуемый для хранения списка.
Пусть имеется линейный список с целыми значениями и для его хранения
используется массив d (с числом элементов 100), а количество элементов в списке
указывается переменной l. Реализация указанных ранее операций над списком
представляется следующими фрагментами программ которые используют объявления:
float d[100];
int i,j,l;
1) печать значения первого элемента (узла)
if (i<0 || i>l) printf("\n нет элемента");
else printf("d[%d]=%f ",i,d[i]);
2) удаление элемента, следующего за i-тым узлом
if (i>=l) printf("\n нет следующего ");
l--;
for (j=i+1;j=l) printf("\n нет соседа");
else printf("\n %d %d",d[i-1],d[i+1]);
4) добавление нового элемента new за i-тым узлом
if (i==l || i>l) printf("\n нельзя добавить");
else
{ for (j=l; j>i+1; j--) d[j+1]=d[j];
d[i+1]=new; l++;
}
5) частичное упорядочение списка с элементами К1,К2,...,Кl в
список K1',K2',...,Ks,K1,Kt",...,Kt", s+t+1=l так, чтобы K1'= K1.
{ int t=1;
float aux;
for (i=2; i<=l; i++)
if (d[i]=2; j--) d[j]=d[j-1];
t++;
d[i]=aux;
}
}
Схема движения индексов i,j,t и значения aux=d[i] при выполнении приведенного
фрагмента программы приведена на рис.15.
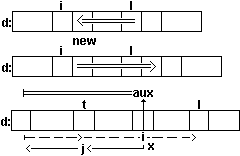
Рис.15. Движение индексов при выполнении операций над
списком в последовательном хранении.
Количество действий Q, требуемых для выполнения приведенных операций над
списком, определяется соотношениями: для операций 1 и 2 - Q=1; для операций
3,4 - Q=l; для операции 5 - Q=l*l.
Заметим, что вообще операцию 5 можно выполнить при количестве действий
порядка l, а операции 3 и 4 для включения и исключения элементов в конце
списка, часто встречающиеся при работе со стеками, - при количестве действий 1.
Более сложная организация операций требуется при размещении в массиве d
нескольких списков, или при размещении списка без привязки его начала к
первому элементу массива.
При простом связанном хранении каждый элемент списка представляет собой
структуру nd, состоящую из двух элементов: val - предназначен для хранения
элемента списка, n - для указателя на структуру, содержащую следующий элемент
списка. На первый элемент списка указывает указатель dl. Для всех операций над
списком используется описание:
typedef struct nd
{ float val;
struct nd * n; } ND;
int i,j;
ND * dl, * r, * p;
Для реализации операций могут использоваться следующие фрагменты программ:
1) печать значения i-го элемента
r=dl;j=1;
while(r!=NULL && j++n ;
if (r==NULL) printf("\n нет узла %d ",i);
else printf("\n элемент %d равен %f ",i,r->val);
2) печать обоих соседей узла(элемента), определяемого указателем p (см.
рис.16)

Рис.16. Схема выбора соседних элементов.
if((r=p->n)==NULL) printf("\n нет соседа справа");
else printf("\n сосед справа %f", r->val);
if(dl==p) printf("\n нет соседа слева" );
else { r=dl;
while( r->n!=p ) r=r->n;
printf("\n левый сосед %f", r->val);
}
3) удаление элемента, следующего за узлом, на который указывает р (см.
рис.17)

Рис.17. Схема удаления элемента из списка.
if ((r=p->n)==NULL) printf("\n нет следующего");
p->n=r->n; free(r->n);
4) вставка нового узла со значением new за элементом, определенным
указателем р (см. рис.18)

Рис.18. Схема вставки элемента в список.
r=malloc(1,sizeof(ND));
r->n=p->n; r->val=new; p->n=r;
5) частичное упорядочение списка в последовательность
значений , s+t+1=l, так что K1'=K1;
после упорядочения указатель v указывает на элемент K1' (см. рис.19)

Рис.19. Схема частичного упорядочения списка.
ND *v;
float k1;
k1=dl->val;
r=dl;
while( r->n!=NULL )
{ v=r->n;
if (v->valn=v->n;
v->n=dl;
dl=v;
}
else r=v;
}
Количество действий, требуемых для выполнения указанных операций над списком
в связанном хранении, оценивается соотношениями: для операций 1 и 2 - Q=l; для
операций 3 и 4 - Q=1; для операции 5 - Q=l.
Связанное хранение линейного списка называется списком с двумя связями или
двусвязным списком, если каждый элемент хранения имеет два компонента указателя
(ссылки на предыдущий и последующий элементы линейного списка).
В программе двусвязный список можно реализовать с помощью описаний:
typedef struct ndd
{ float val; /* значение элемента */
struct ndd * n; /* указатель на следующий элемент */
struct ndd * m; /* указатель на предыдующий элемент */
} NDD;
NDD * dl, * p, * r;
Графическая интерпретация метода связанного хранения списка F=< 2,5,7,1 >
как списка с двумя связями приведена на рис.20.

Рис.20. Схема хранения двусвязного списка.
Вставка нового узла со значением new за элементом, определяемым указателем p,
осуществляется при помощи операторов:
r=malloc(NDD);
r->val=new;
r->n=p->n;
(p->n)->m=r;
p->=r;
Удаление элемента, следующего за узлом, на который указывает p
p->n=r;
p->n=(p->n)->n;
( (p->n)->n )->m=p;
free(r);
Связанное хранение линейного списка называется циклическим списком, если
его последний указывает на первый элемент, а указатель dl - на последний
элемент списка.
Схема циклического хранение списка F=< 2,5,7,1 > приведена на рис.21.
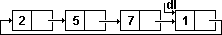
Рис.21. Схема циклического хранения списка.
При решении конкретных задач могут возникать разные виды связанного хранения.
Пусть на входе задана последовательность целых чисел B1,B2,...,Bn из
интервала от 1 до 9999, и пусть Fi (1 по возрастанию. Составить
процедуру для формирования Fn в связанном хранении и возвращения указателя на
его начало.
При решении задачи в каждый момент времени имеем упорядоченный список Fi и
при вводе элемента Bi+1 вставляем его в нужное место списка Fi, получая
упорядоченный список Fi+1. Здесь возможны три варианта: в списке нет элементов;
число вставляется в начало списка; число вставляется в конец списка. Чтобы
унифицировать все возможные варианты, начальный список организуем как связанный
список из двух элементов <0,1000>.
Рассмотрим программу решения поставленной задачи, в которой указатели dl,
r, p, v имеют следующее значение: dl указывает начало списка; p, v - два
соседних узла; r фиксирует узел, содержащий очередное введенное значение in.
#include
#include
typedef struct str1
{ float val;
struct str1 *n; } ND;
main()
{ ND *arrange(void);
ND *p;
p=arrange();
while(p!=NULL)
{
printf("\n %f ",p->val);
p=p->n;
}
}
ND *arrange() /* формирование упорядоченного списка */
{ ND *dl, *r, *p, *v;
float in=1;
char *is;
dl=malloc(sizeof(ND));
dl->val=0; /* первый элемент */
dl->n=r=malloc(sizeof(ND));
r->val=10000; r->n=NULL; /* последний элемент */
while(1)
{
scanf(" %s",is);
if(* is=='q') break;
in=atof(is);
r=malloc(sizeof(ND));
r->val=in;
p=dl;
v=p->n;
while(v->valn;
}
r->n=v;
p->n=r;
}
return(dl);
}
В зависимости от метода доступа к элементам линейного списка различают
разновидности линейных списков называемые стеком, очередью и двусторонней
очередью.
Стек - это конечная последовательность некоторых однотипных элементов -
скалярных переменных, массивов, структур или объединений, среди которых могут
быть и одинаковые. Стек обозначается в виде: S= и представляет
динамическую структуру данных; ее количество элементов заранее не указывается
и в процессе работы, как правило изменяется. Если в стеке элементов нет, то он
называется пустым и обозначается S=< >.
Допустимыми операциями над стеком являются:
- проверка стека на пустоту S=< >,
- добавление нового элемента Sn+1 в конец стека - преобразование
< S1,...,Sn> в < S1,...,Sn+1>;
- изъятие последнего элемента из стека - преобразование < S1,...,Sn-1,Sn>
в < S1,...,Sn-1>;
- доступ к его последнему элементу Sn, если стек не пуст.
Таким образом, операции добавления и удаления элемента, а также доступа к
элементу выполняются только в конце списка. Стек можно представить как стопку
книг на столе, где добавление или взятие новой книги возможно только сверху.
Очередь - это линейный список, где элементы удаляются из начала списка, а
добавляются в конце списка (как обыкновенная очередь в магазине).
Двусторонняя очередь - это линейный список, у которого операции добавления
и удаления элементов и доступа к элементам возможны как вначале так и в конце
списка. Такую очередь можно представить как последовательность книг стоящих на
полке, так что доступ к ним возможен с обоих концов.
Реализация стеков и очередей в программе может быть выполнена в виде
последовательного или связанного хранения. Рассмотрим примеры организации
стека этими способами.
Одной из форм представления выражений является польская инверсная запись,
задающая выражение так, что операции в нем записываются в порядке выполнения,
а операнды находятся непосредственно перед операцией.
Например, выражение
(6+8)*5-6/2
в польской инверсной записи имеет вид
6 8 + 5 * 6 2 / -
Особенность такой записи состоит в том, что значение выражения можно
вычислить за один просмотр записи слева направо, используя стек, который до
этого должен быть пуст. Каждое новое число заносится в стек, а операции
выполняются над верхними элементами стека, заменяя эти элементы результатом
операции. Для приведенного выражения динамика изменения стека будет иметь вид
S = < >; <6>; <6,8>; <14>; <14,5>; <70>;
<70,6>; <70,6,2>; <70,3>; <67>.
Ниже приведена функция eval, которая вычисляет значение выражения, заданного
в массиве m в форме польской инверсной записи, причем m[i]>0 означает
неотрицательное число, а значения m[i]<0 - операции. В качестве кодировки
операций сложения, вычитания, умножения и деления выбраны отрицательные числа
-1, -2, -3, -4. Для организации последовательного хранения стека используется
внутренний массив stack. Параметрами функции являются входной массив a и его
длина l.
float eval (float *m, int l)
{ int p,n,i;
float stack[50],c;
for(i=0; i < l ;i++)
if ((n=m[i])<0)
{ c=st[p--];
switch(n)
{ case -1: stack[p]+=c; break;
case -2: stack[p]-=c; break;
case -3: stack[p]*=c; break;
case -4: stack[p]/=c;
}
}
else stack[++p]=n;
return(stack[p]);
}
Рассмотрим другую задачу. Пусть требуется ввести некоторую последовательность
символов, заканчивающуюся точкой, и напечатать ее в обратном порядке (т.е. если
на входе будет "ABcEr-1." то на выходе должно быть "1-rEcBA"). Представленная
ниже программа сначала вводит все символы последовательности, записывая их в
стек, а затем содержимое стека печатается в обратном порядке. Это основная
особенность стека - чем позже элемент занесен в стек, тем раньше он будет
извлечен из стека. Реализация стека выполнена в связанном хранении при помощи
указателей p и q на тип, именованный именем STACK.
#include
typedef struct st /* объявление типа STACK */
{ char ch;
struct st *ps; } STACK;
main()
{ STACK *p,*q;
char a;
p=NULL;
do /* заполнение стека */
{ a=getch();
q=malloc(sizeof(STR1));
q->ps=p; p=q;
q->ch=a;
} while(a!='.');
do /* печать стека */
{ p=q->ps;free(q);q=p;
printf("%c",p->ch);
} while(p->ps!=NULL);
}
При хранении больших объемов информации в форме линейных списков
нежелательно хранить элементы с одинаковым значением, поэтому используют
различные методы сжатия списков.
Сжатое хранение. Пусть в списке B= несколько элементов имеют
одинаковое значение V, а список B'= получается из B заменой
каждого элемента Ki на пару Ki'=(i,Ki). Пусть далее B"=< K1",K2",...,Km" > -
подсписок B', получающийся вычеркиванием всех пар Ki=(i,V). Сжатым хранением В
является метод хранения В", в котором элементы со значением V умалчиваются.
Различают последовательное сжатое хранение и связанное сжатое хранение.
Например, для списка B=, содержащего несколько узлов со
значением Х, последовательное сжатое и связанное сжатое хранения, с умалчиванием
элементов со значением Х, представлены на рис.22,23.
1,C
| 3,Y
| 6,S
| 7,H
| 9,T
|
| Рис.22. Последовательное сжатое хранение списка. |
|---|
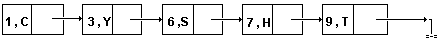
Рис.23. Связное сжатое хранение списка.
Достоинство сжатого хранения списка при большом числе элементов со значением
V заключается в возможности уменьшения объема памяти для его хранения.
Поиск i-го элемента в связанном сжатом хранении осуществляется методом
полного просмотра, при последовательном хранении - методом бинарного поиска.
Преимущества и недостатки последовательного сжатого и связанного сжатого
хранений аналогичны преимуществам и недостаткам последовательного и связанного
хранений.
Рассмотрим следующую задачу. На входе заданы две последовательности целых
чисел M=< M1,M2,...,M10000 >, N=< N1,N2,...,N10000 >, причем 92% элементов
последовательности М равны нулю. Составить программу для вычисления суммы
произведений Mi * Ni, i=1,2,...,10000.
Предположим, что список М хранится последовательно сжато в массиве структур
m с объявлением:
struct
{ int nm;
float val; } m[10000];
Для определения конца списка добавим еще один элемент с порядковым номером
m[j].nm=10001, который называется стоппером (stopper) и располагается за
последним элементом сжатого хранения списка в массиве m.
Программа для нахождения искомой суммы имеет вид:
# include
main()
{ int i,j=0;
float inp,sum=0;
struct /* объявление массива */
{ int nm; /* структур */
float val; } m[10000];
for(i=0;i<10000;i++) /* чтение списка M */
{ scanf("%f",&inp);
if (inp!=0)
{ m[j].nm=i;
m[j++].val=inp;
}
}
m[j].nm=10001; /* stopper */
for(i=0,j=0; i<10000; i++)
{ scanf("%f",&inp); /* чтение списка N */
if(i==m[j].nm) /* вычисление суммы */
sum+=m[j++].val*inp;
}
printf( "сумма произведений Mi*Ni равна %f",sum);
}
Индексное хранение используется для уменьшения времени поиска нужного
элемента в списке и заключается в следующем. Исходный список B =
< K1,K2, ...,Kn > разбивается на несколько подсписков В1,В2, ...,Вm таким
образом, что каждый элемент списка В попадает только в один из подсписков, и
дополнительно используется индексный список с М элементами, указывающими на
начало списков В1,В2, ...,Вm.
Считается, что список хранится индексно с помощью подсписков B1,B2, ...,Bm
и индексного спискa X = < ADG1,ADG2,... ADGm >, где ADGj - адрес начала
подсписка Bj, j=1,M.
При индексном хранении элемент К подсписка Bj имеет индекс j. Для получения
индексного хранения исходный список В часто преобразуется в список В' путем
включения в каждый узел еще и его порядкового номера в исходном списке В, а в
j-ый элемент индексного списка Х, кроме ADGj, может включаться некоторая
дополнительная информация о подсписке Bj. Разбиение списка В на подсписки
осуществляется так, чтобы все элементы В, обладающие определенным свойством Рj,
попадали в один подсписок Bj.
Достоинством индексного хранения является то, что для нахождения элемента К
с заданным свойством Pj достаточно просмотреть только элементы подсписка Bj; его
начало находится по индексному списку Х, так как для любого К, принадлежащего
Bi, при i не равном j свойство Pj не выполняется.
В разбиении В часто используется индексная функция G(K), вычисляющая по
элементу К его индекс j, т.е. G(K)=j. Функция G обычно зависит от позиции К,
обозначаемой поз.K, в подсписке В или от значения определенной части компоненты
К - ее ключа.
Рассмотрим список B=< K1,K2, ...,K9 > с элементами
К1=(17,Y), K2=(23,H), K3=(60,I), K4=(90,S), K5=(66,T),
K6=(77,T), K7=(50,U), K8=(88,W), K9=(30,S).
Если для разбиения этого списка на подсписки в качестве индексной функции
взять Ga(K)=1+(поз.K-1)/3, то список разделится на три подсписка:
B1a=<(17,Y),(23,H),(60,I)>,
B2a=<(90,S),(66,T),(77,T)>,
B3a=<(50,U),(88,W),(30,S)>.
Добавляя всюду еще и начальную позицию элемента в списке, получаем:
B1a'=<(1,17,Y),(2,23,H),(3,60,I)>,
B2a'=<(4,90,S),(5,66,T),(6,77,T)>,
B3a'=<(7,50,U),(8,88,W),(9,30,S)>.
Если в качестве индексной функции выбрать другую функцию Gb(K)=1+(поз.K-1)%3,
то получим списки:
B1b"=<(1,17,Y),(4,90,S),(7,50,U)>,
B2b"=<(2,23,H),(5,66,T),(8,88,U)>,
B3b"=<(3,60,I),(6,77,T),(9,30,S)>.
Теперь для нахождения узла K6 достаточно просмотреть только одну из трех
последовательностей (списков). При использовании функции Ga(K) это список B2a',
а при функции Gb(K) список B3b".
Для индексной функции Gc(K)=1+K1/100, где K1 - первая компонента элемента К,
находим:
B1=<(17,Y),(23,H),(60,I),(90,S)>,
B2=<(66,T),(77,T)>,
B3=<(50,U),(88,W)>,
B4=<(30,S)>.
Чтобы найти здесь узел К с первым компонентом-ключом К1=77, достаточно
просмотреть список B2.
При реализации индексного хранения применяется методика А для хранения
индексного списка Х (функция Ga(X) ) и методика C для хранения подсписков
B1,B2,...,Bm (функция Gc(Bi)), т.е. используется, так называемое, A-C индексное
хранение.
В практике часто используется последовательно-связанное индексное хранение.
Так как обычно длина списка индексов известна, то его удобно хранить
последовательно, обеспечивая прямой доступ к любому элементу списка индексов.
Подсписки B1,B2,...,Bm хранятся связанно, что упрощает вставку и удаление
узлов(элементов). В частности, подобный метод хранения используется в ЕС ЭВМ
для организации, так называемых, индексно-последовательных наборов данных, в
которых доступ к отдельным записям возможен как последовательно, так и при
помощи ключа.
Последовательно-связанное индексное хранение для приведенного примера
изображено на рис.24, где X=.
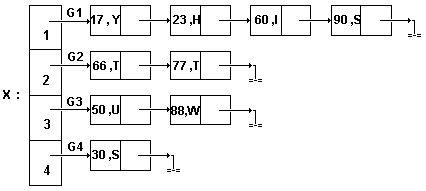
Рис.24. Последовательно-связанное индексное хранение списка.
Рассмотрим еще одну задачу. На входе задана последовательность целых
положительных чисел, заканчивающаяся нулем. Составить процедуру для ввода этой
последовательности и организации ее последовательно-связанного индексного
хранения таким образом, чтобы числа, совпадающие в двух последних цифрах,
помещались в один подсписок.
Выберем в качестве индексной функции G(K)=K%100+1, а в качестве индексного
списка Х - массив из 100 элементов. Следующая функция решает поставленную
задачу:
#include
#include
typedef struct nd
{ float val;
struct nd *n; } ND;
int index (ND *x[100])
{ ND *p;
int i,j=0;
float inp;
for (i=0; i<100; i++) x[i]=NULL;
scanf("%d",&inp);
while (inp!=0)
{ j++;
p=malloc(sizeof(ND));
i=inp%100+1;
p->val=inp;
p->n=x[i];
x[i]=p;
scanf("%d",&inp);
}
return j;
}
Возвращаемым значением функции index будет число обработанных элементов
списка.
Для индексного списка также может использоваться индексное хранение. Пусть,
например, имеется список B= с элементами
K1=(338,Z), K2=(145,A), K3=(136,H), K4=(214,I), K5 =(146,C),
K6=(334,Y), K7=(333,P), K8=(127,G), K9=(310,O), K10=(322,X).
Требуется разделить его на семь подсписков, т.е. X= таким
образом, чтобы в каждый список B1,B2,...,B7 попадали элементы, совпадающие в
первой компоненте первыми двумя цифрами. Список Х, в свою очередь, будем
индексировать списком индексов Y=, чтобы в каждый список Y1,Y2,Y3
попадали элементы из X, у которых в первой компоненте совпадают первые цифры.
Если списки B1,B2,...,B7 хранить связанно, а списки индексов X,Y индексно, то
такой способ хранения списка B называется связанно-связанным связанным
индексным хранением. Графическое изображение этого хранения приведено на рис.25.
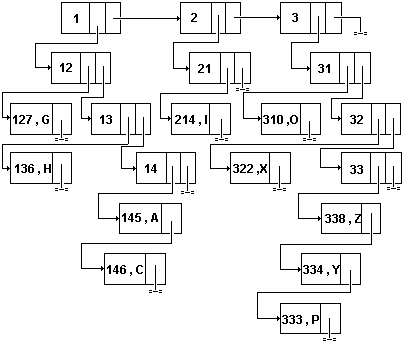
Рис.25. Связанно-связанное связанное индексное хранение списка.
[ Назад | Оглавление | Вперед ]
Copyright © CIT